Simula un oscilador forzado en Mathematica: domina su funcionamiento
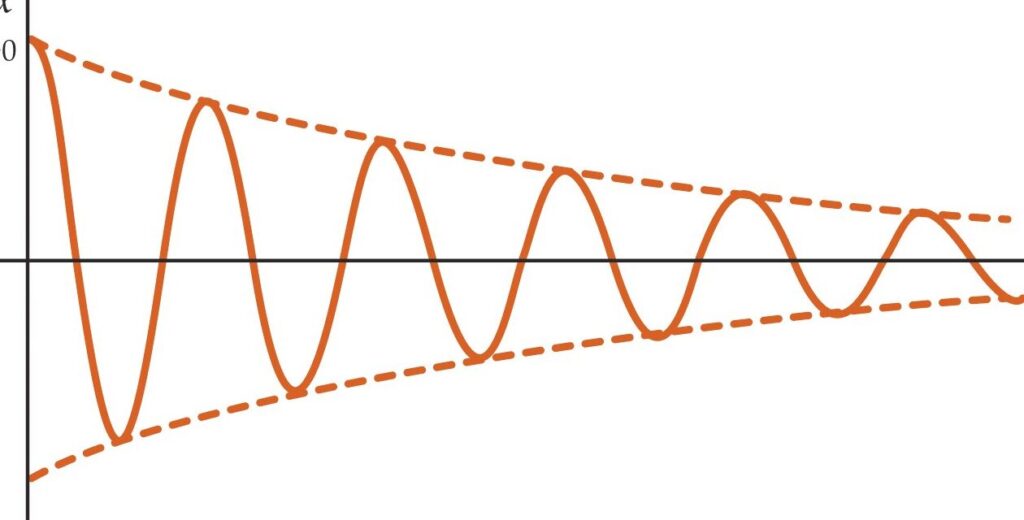
El estudio de los osciladores forzados es esencial en el campo de la física y la ingeniería. Estos sistemas son capaces de responder a fuerzas externas, lo que genera una respuesta que puede ser compleja y fascinante. Para comprender mejor su funcionamiento, es útil utilizar herramientas de simulación, como el software Mathematica, que nos permite visualizar y analizar el comportamiento de estos sistemas en tiempo real.
Exploraremos cómo simular un oscilador forzado en Mathematica y cómo interpretar los resultados obtenidos. Veremos cómo ajustar los parámetros de la fuerza externa para obtener diferentes respuestas y cómo analizar la amplitud y frecuencia de oscilación resultantes. Además, conoceremos algunos trucos y técnicas avanzadas para dominar por completo el funcionamiento de un oscilador forzado.
¿Qué verás en este artículo?
- Cómo se define un oscilador forzado en física y qué lo hace diferente de un oscilador libre
- Cuáles son los principales conceptos y ecuaciones utilizados para describir el comportamiento de un oscilador forzado
- Qué parámetros y variables se deben tener en cuenta al simular un oscilador forzado en Mathematica
- Cuál es el código básico necesario para simular un oscilador forzado en Mathematica
- Cómo se pueden visualizar los resultados de la simulación de un oscilador forzado en Mathematica
- Cuáles son algunos ejemplos prácticos en los que se puede aplicar un oscilador forzado y cómo puede ayudar a entender ciertos fenómenos físicos
- Qué herramientas o paquetes adicionales en Mathematica se pueden utilizar para mejorar las simulaciones de osciladores forzados
- Cuáles son algunas aplicaciones más avanzadas de la simulación de osciladores forzados en Mathematica
- Existe alguna forma de optimizar o acelerar las simulaciones de osciladores forzados en Mathematica
- Qué recursos adicionales se pueden utilizar para aprender más sobre la simulación de osciladores forzados en Mathematica
-
Preguntas frecuentes (FAQ)
- ¿Puedo simular cualquier tipo de oscilador forzado en Mathematica?
- ¿Cuáles son los pasos para simular un oscilador forzado en Mathematica?
- ¿Es necesario conocer programación para simular un oscilador forzado en Mathematica?
- ¿Qué tipos de gráficos puedo obtener al simular un oscilador forzado en Mathematica?
- ¿Puedo simular sistemas con más de un oscilador forzado en Mathematica?
Cómo se define un oscilador forzado en física y qué lo hace diferente de un oscilador libre
En física, un oscilador forzado es aquel sistema que se encuentra sometido a una fuerza externa que lo impulsa a oscilar. A diferencia de un oscilador libre, que oscila de manera autónoma sin la influencia de fuerzas externas, el oscilador forzado tiene una frecuencia de oscilación determinada por la fuerza impuesta sobre él.
El comportamiento de un oscilador forzado puede describirse mediante una ecuación diferencial que combina los términos del oscilador libre y la fuerza externa aplicada. Esta ecuación permite determinar cómo la fuerza externa afecta la amplitud y la fase del oscilador, así como su respuesta en función de la frecuencia de la fuerza aplicada.
En el estudio de osciladores forzados, es común utilizar el software Mathematica para simular y analizar su comportamiento. Mathematica ofrece una amplia gama de herramientas y funciones que facilitan la modelización y visualización de los osciladores forzados, permitiendo una comprensión más profunda de su funcionamiento.
Cuáles son los principales conceptos y ecuaciones utilizados para describir el comportamiento de un oscilador forzado
El estudio del comportamiento de los osciladores forzados es fundamental en la física y la ingeniería. Para describir este fenómeno, se utilizan varios conceptos y ecuaciones clave.
En primer lugar, es importante entender qué es un oscilador forzado. Un oscilador es un sistema físico que exhibe un movimiento periódico alrededor de una posición de equilibrio. En el caso de un oscilador forzado, este movimiento es impulsado por una fuerza externa en forma de una función periódica.
La ecuación diferencial que describe el comportamiento de un oscilador forzado es la ecuación de movimiento. En su forma más general, esta ecuación se puede escribir como:
mx''(t) + bx'(t) + kx(t) = F(t)
En esta ecuación, m es la masa del oscilador, x(t) es la posición del oscilador en función del tiempo, b es el coeficiente de amortiguamiento, k es la constante del resorte y F(t) es la función que representa la fuerza externa.
Qué parámetros y variables se deben tener en cuenta al simular un oscilador forzado en Mathematica
Al simular un oscilador forzado en Mathematica, es importante considerar varios parámetros y variables que afectan su comportamiento. Uno de los parámetros clave es la frecuencia natural del oscilador, representada por la variable ω₀.
Otro parámetro importante es la frecuencia de la fuerza externa, representada por la variable ω. Esta frecuencia determina cómo interactúa la fuerza externa con el oscilador y puede influir en su amplitud y fase.
Además, es fundamental tener en cuenta la constante de amortiguamiento del oscilador, denotada como γ. Esta constante determina la resistencia al movimiento del oscilador y puede afectar su amplitud y período.
Por último, pero no menos importante, se deben considerar las condiciones iniciales del oscilador, como la posición inicial y la velocidad inicial. Estas condiciones determinan el estado inicial del oscilador y pueden afectar su respuesta a la fuerza externa.
Al simular un oscilador forzado en Mathematica, es esencial tener en cuenta parámetros como la frecuencia natural, la frecuencia de la fuerza externa, la constante de amortiguamiento y las condiciones iniciales. Estos factores determinan en gran medida el comportamiento del oscilador y nos permiten comprender y dominar su funcionamiento.
Cuál es el código básico necesario para simular un oscilador forzado en Mathematica
Para simular un oscilador forzado en Mathematica, necesitarás familiarizarte con el uso de la función "NDSolve". Esta función es esencial cuando se trata de resolver ecuaciones diferenciales en Mathematica. En el caso de un oscilador forzado, utilizaremos un sistema de ecuaciones diferenciales de segundo orden que describe la dinámica del sistema.
El primer paso es definir las ecuaciones diferenciales que describen el oscilador forzado. Por ejemplo, si tenemos un oscilador armónico simple con una fuerza externa sinusoidal, las ecuaciones diferenciales se pueden escribir como:
eqs = {x'' + kx == ACos, x == x0, x' == v0}
Donde "x" es la posición del oscilador en función del tiempo, "k" es la constante del resorte, "A" es la amplitud de la fuerza externa, "ω" es la frecuencia angular de la fuerza externa, "x0" es la posición inicial del oscilador y "v0" es la velocidad inicial del oscilador.
Luego, puedes utilizar la función "NDSolve" para resolver estas ecuaciones diferenciales y obtener la solución numérica del oscilador forzado. Por ejemplo:
sol = NDSolve;
Esto te dará la solución "x" en el intervalo de tiempo de 0 a 10. Puedes ajustar los valores iniciales y los parámetros del sistema según tus necesidades.
Una vez que hayas obtenido la solución numérica, puedes utilizar la función "Plot" para visualizar la posición del oscilador en función del tiempo. Por ejemplo:
Plot /. sol, {t, 0, 10}, PlotRange -> All]
Esto generará un gráfico de la posición del oscilador en función del tiempo, donde puedes observar cómo se ve afectado por la fuerza externa.
Simular un oscilador forzado en Mathematica requiere la definición de las ecuaciones diferenciales que describen el sistema, utilizando la función "NDSolve" para obtener la solución numérica y luego utilizando la función "Plot" para visualizar los resultados. Con estos pasos básicos, puedes empezar a explorar y dominar el funcionamiento de los osciladores forzados en Mathematica.
Cómo se pueden visualizar los resultados de la simulación de un oscilador forzado en Mathematica
La visualización de los resultados de la simulación de un oscilador forzado en Mathematica es esencial para comprender el comportamiento del sistema. En este artículo, aprenderás cómo lograrlo de manera efectiva utilizando las herramientas y funciones proporcionadas por Mathematica.
Utilizando la función Plot para graficar el desplazamiento del oscilador en función del tiempo
Una de las formas más comunes de visualizar los resultados de la simulación es a través de un gráfico que muestra el desplazamiento del oscilador en función del tiempo. Para ello, podemos hacer uso de la función Plot de Mathematica. Esta función nos permite representar una función matemática en un gráfico 2D.
Para utilizar la función Plot, primero debemos definir la función que describe el movimiento del oscilador forzado. Por ejemplo, si el oscilador está sometido a una fuerza externa sinusoidal, la función podría ser de la forma Asin(wt), donde A es la amplitud y w es la frecuencia angular de la fuerza externa.
A continuación, podemos utilizar la función Plot de la siguiente manera:
Plot
Donde tmin y tmax son los límites de tiempo para los cuales queremos visualizar el desplazamiento del oscilador.
Utilizando la función ParametricPlot para graficar el espacio de fases del oscilador forzado
Otra forma útil de visualizar los resultados de la simulación de un oscilador forzado es a través del espacio de fases. El espacio de fases es una representación gráfica de las variables de estado de un sistema dinámico.
En Mathematica, podemos utilizar la función ParametricPlot para generar un gráfico del espacio de fases del oscilador forzado. Esta función nos permite representar una parametrización de una curva en un plano.
Para utilizar la función ParametricPlot, debemos definir las ecuaciones diferenciales que describen el movimiento del oscilador forzado en términos de sus variables de estado. Por ejemplo, si el oscilador está descrito por las ecuaciones dx/dt = v y dv/dt = -kx - bv + Fsin(wt), donde x es el desplazamiento, v es la velocidad, k es la constante del resorte, b es el coeficiente de amortiguamiento, F es la amplitud de la fuerza externa y w es la frecuencia angular de la fuerza externa, podemos utilizar la función ParametricPlot de la siguiente manera:
ParametricPlot == v, v' == -kx - bv + Fsin(wt), x == x0, v == v0}, {x, v}, {t, tmin, tmax}]], {x, xmin, xmax}, {v, vmin, vmax}]
Donde x0 y v0 son las condiciones iniciales del oscilador y xmin, xmax, vmin y vmax son los límites para los cuales queremos visualizar el espacio de fases.
Estas son solo algunas de las formas en las que se pueden visualizar los resultados de la simulación de un oscilador forzado en Mathematica. Con estas herramientas y funciones, podrás dominar el funcionamiento del oscilador y comprender mejor su comportamiento.
Cuáles son algunos ejemplos prácticos en los que se puede aplicar un oscilador forzado y cómo puede ayudar a entender ciertos fenómenos físicos
El oscilador forzado es un concepto ampliamente utilizado en la física y tiene numerosas aplicaciones prácticas. Uno de los ejemplos más comunes es el oscilador de péndulo simple, donde un péndulo con una masa suspendida oscila hacia adelante y hacia atrás bajo la acción de la gravedad. Al aplicar una fuerza periódica externa, como un motor, al péndulo, estamos forzando el sistema y podemos estudiar cómo varía su movimiento en respuesta a esta fuerza.
En otros campos de la física, el oscilador forzado también se utiliza para comprender fenómenos como la resonancia mecánica. Por ejemplo, en la ingeniería estructural, se puede estudiar la respuesta de un puente a las vibraciones causadas por el viento mediante el análisis de un oscilador forzado. Esto permite determinar si la estructura resonará y cómo afectará esto a su estabilidad y durabilidad.
Además, en la física cuántica, el oscilador forzado se utiliza para comprender cómo los electrones se comportan en presencia de un campo electromagnético. Esto es fundamental para el desarrollo de tecnologías como la resonancia magnética y la espectroscopia, que se utilizan en medicina y química para obtener información detallada sobre las propiedades de las moléculas y los tejidos.
El oscilador forzado es un concepto crucial en la física y tiene aplicaciones prácticas en una amplia gama de campos. Su estudio permite comprender mejor cómo los sistemas físicos responden a fuerzas externas y cómo podemos utilizar esto para mejorar nuestra comprensión de los fenómenos naturales y desarrollar tecnologías innovadoras.
Qué herramientas o paquetes adicionales en Mathematica se pueden utilizar para mejorar las simulaciones de osciladores forzados
Existen varias herramientas y paquetes adicionales en Mathematica que pueden ayudarte a mejorar tus simulaciones de osciladores forzados. Uno de ellos es el paquete Control System Toolbox, el cual te permite diseñar y analizar sistemas de control en tiempo continuo y discreto.
Otra herramienta útil es el paquete Symbolic Control Toolbox, que te permite realizar análisis simbólicos de sistemas de control y obtener soluciones analíticas.
También puedes utilizar el paquete NDSolve para resolver numéricamente ecuaciones diferenciales que modelen el comportamiento de osciladores forzados. NDSolve te permite especificar condiciones iniciales y condiciones de contorno, y obtener soluciones aproximadas en forma de gráficas.
Además, puedes utilizar funciones como FourierTransform y LaplaceTransform para analizar el espectro de frecuencias y la respuesta en frecuencia de los osciladores forzados.
Hay una variedad de herramientas y paquetes adicionales en Mathematica que te permiten mejorar tus simulaciones de osciladores forzados, desde el diseño y análisis de sistemas de control hasta la resolución numérica de ecuaciones diferenciales y el análisis del espectro de frecuencias.
Cuáles son algunas aplicaciones más avanzadas de la simulación de osciladores forzados en Mathematica
La simulación de osciladores forzados en Mathematica tiene muchas aplicaciones avanzadas en diversos campos. Una de ellas es en la física, donde se pueden simular osciladores forzados en sistemas mecánicos, como puentes colgantes, para analizar su respuesta ante diferentes frecuencias de excitación y amplitudes de fuerza.
En ingeniería mecánica, la simulación de osciladores forzados en Mathematica puede utilizarse para analizar el comportamiento de sistemas vibrantes, como motores, y optimizar su funcionamiento. También se pueden simular osciladores forzados en sistemas eléctricos, como circuitos resonantes, para estudiar su respuesta ante señales de entrada y analizar la transferencia de energía.
Otra aplicación interesante es en biología, donde se pueden simular osciladores forzados en modelos matemáticos de sistemas biológicos, como el ritmo cardíaco o el reloj circadiano, y estudiar cómo la fuerza externa afecta su comportamiento.
Existe alguna forma de optimizar o acelerar las simulaciones de osciladores forzados en Mathematica
Cuando trabajamos con osciladores forzados en Mathematica, puede ser frustrante enfrentarse a simulaciones que toman mucho tiempo en ejecutarse. Sin embargo, hay algunas técnicas que podemos utilizar para optimizar y acelerar estas simulaciones.
Una de ellas es aprovechar al máximo las funciones y capacidades de programación funcional de Mathematica. Esto implica utilizar constructores como Table o Map en lugar de bucles explícitos, lo que podría agilizar considerablemente el proceso.
Otra estrategia es reducir la resolución temporal de la simulación, es decir, disminuir la cantidad de puntos que calculamos en cada paso del tiempo. Esto puede resultar en una simulación más rápida, aunque menos precisa. Dependerá del caso particular decidir si esta aproximación es adecuada.
También es importante tener en cuenta el uso eficiente de recursos del sistema. Esto implica liberar memoria y variables no utilizadas y evitar realizar cálculos innecesarios o redundantes.
Optimizar y acelerar las simulaciones de osciladores forzados en Mathematica implica utilizar técnicas de programación funcional, ajustar la resolución temporal y gestionar eficientemente los recursos del sistema. Con estas estrategias, podrás dominar el funcionamiento de los osciladores forzados de una manera más eficiente y efectiva.
Qué recursos adicionales se pueden utilizar para aprender más sobre la simulación de osciladores forzados en Mathematica
Para aprender más sobre la simulación de osciladores forzados en Mathematica, existen varios recursos adicionales que pueden ser útiles. Uno de ellos son los tutoriales en línea ofrecidos por la comunidad de usuarios de Mathematica. Estos tutoriales proporcionan una introducción paso a paso sobre cómo simular y analizar osciladores forzados utilizando la plataforma de Mathematica.
Otro recurso valioso es la documentación oficial de Mathematica. Allí encontrarás una gran cantidad de información detallada sobre las funciones y comandos específicos utilizados para la simulación de osciladores forzados. Esta documentación incluye ejemplos de código, explicaciones detalladas y referencias cruzadas para ayudarte a comprender y aplicar los conceptos de manera efectiva.
Además, puedes encontrar libros y artículos especializados que tratan sobre la simulación de osciladores forzados en Mathematica. Estos recursos proporcionan un enfoque más profundo y teórico sobre el tema, lo que puede ser útil si deseas tener un conocimiento más completo y sólido. Algunos de estos libros incluso ofrecen ejercicios prácticos y problemas para resolver, lo que te permitirá poner en práctica tus habilidades de simulación.
Por último, otra forma de aprender más sobre la simulación de osciladores forzados en Mathematica es a través de cursos en línea o talleres presenciales. Estos cursos suelen ser impartidos por expertos en la materia y te brindan la oportunidad de interactuar directamente con el instructor y otros estudiantes. Además, algunos de estos cursos ofrecen proyectos prácticos donde podrás aplicar tus conocimientos en la simulación de osciladores forzados en situaciones del mundo real.
Preguntas frecuentes (FAQ)
¿Puedo simular cualquier tipo de oscilador forzado en Mathematica?
Sí, Mathematica es una herramienta muy versátil que te permite simular cualquier tipo de oscilador forzado.
¿Cuáles son los pasos para simular un oscilador forzado en Mathematica?
Los pasos son: definir las ecuaciones diferenciales del sistema, establecer las condiciones iniciales y los parámetros del sistema, y finalmente, utilizar las funciones de integración numérica de Mathematica para obtener las soluciones.
¿Es necesario conocer programación para simular un oscilador forzado en Mathematica?
No necesariamente, aunque tener conocimientos básicos de programación puede ser útil para personalizar y optimizar la simulación.
¿Qué tipos de gráficos puedo obtener al simular un oscilador forzado en Mathematica?
Puedes obtener gráficos de las soluciones en función del tiempo, gráficos de fases, diagramas de bifurcación, entre otros.
¿Puedo simular sistemas con más de un oscilador forzado en Mathematica?
Sí, Mathematica te permite simular sistemas con múltiples osciladores forzados y analizar la interacción entre ellos.
Suma las filas de una matriz fácilmente con Mathematica
Aprende a calcular integrales dobles con Wolfram Mathematica
Escribe y borra variables globales en Mathematica: guía práctica
Aprende cómo poner el coseno en Mathematica y obtener su valor
Aprende a añadir celdas en Mathematica de manera sencilla y rápida
Calcula derivadas parciales con Mathematica en minutos
Aprende a unir puntos y crear curvas en Mathematica fácilmente
Cómo representar puntos en Mathematica: tutorial paso a paso
Aprende cómo escribir funciones en trozos en Mathematica
Deja una respuesta
Artículos que podrían interesarte