Resuelve ecuaciones en Mathematica: Despeja x0 fácilmente

Mathematica es un potente software de cálculo matemático utilizado por científicos, ingenieros y matemáticos de todo el mundo. Una de las funcionalidades más útiles de Mathematica es su capacidad para resolver ecuaciones de manera rápida y precisa, lo que facilita en gran medida el trabajo de aquellos que necesitan encontrar soluciones a problemas matemáticos complejos.

Exploraremos cómo utilizar Mathematica para resolver ecuaciones y despejar la variable x0. Veremos paso a paso cómo ingresar la ecuación en el programa, cómo indicar qué variable queremos despejar y cómo obtener la solución deseada. Además, mostraremos algunos ejemplos prácticos para ilustrar su aplicación en situaciones reales.

Cuáles son las principales ventajas de usar Mathematica para resolver ecuaciones

Mathematica es una poderosa herramienta para resolver ecuaciones algebraicas y diferenciales. Su capacidad para manejar cálculos simbólicos la convierte en una opción ideal para resolver ecuaciones de manera rápida y precisa.

Una de las principales ventajas de usar Mathematica es su capacidad para resolver ecuaciones de manera automática. Con solo ingresar la ecuación, Mathematica puede encontrar las soluciones exactas o aproximadas, ahorrando tiempo y esfuerzo en cálculos manuales.

Otra ventaja es su capacidad para manejar ecuaciones simbólicas, lo que significa que puede trabajar con variables en lugar de números específicos. Esto permite obtener soluciones generales que se pueden aplicar a diferentes situaciones.

Además, Mathematica ofrece una amplia gama de funciones y herramientas para manipular ecuaciones. Puede simplificar ecuaciones, resolver sistemas de ecuaciones lineales y no lineales, y realizar operaciones como derivación e integración simbólica.

Por último, Mathematica proporciona una visualización gráfica de las soluciones de las ecuaciones. Esto facilita la comprensión de los resultados y puede ser útil en la presentación de datos.

Cómo puedo despejar la variable "x0" utilizando Mathematica

Si estás buscando una forma sencilla y efectiva de despejar la variable "x0" utilizando Mathematica, estás en el lugar correcto. En este artículo, te mostraré paso a paso cómo resolver ecuaciones y despejar la incógnita "x0" utilizando esta poderosa herramienta.

Paso 1: Definir la ecuación

Lo primero que debes hacer es definir la ecuación en la que deseas despejar la variable "x0". Puedes hacerlo de la siguiente manera:

eqn = TuEcuacion

Reemplaza "TuEcuacion" por la ecuación real que deseas resolver. Asegúrate de utilizar el operador de igualdad ("==") en lugar del operador de asignación ("="). Esto le indicará a Mathematica que quieres resolver la ecuación.

Paso 2: Resolver la ecuación

Una vez que hayas definido la ecuación, puedes utilizar la función "Solve" para resolverla y despejar la variable "x0". Aquí tienes la sintaxis básica:

Solve

Donde "eqn" es la ecuación que definiste en el paso anterior, y "x0" es la variable que deseas despejar. Al ejecutar esta línea de código, Mathematica buscará una solución para la ecuación y te mostrará el resultado.

Paso 3: Interpretar el resultado

Una vez que hayas ejecutado la función "Solve", Mathematica te mostrará el resultado de la ecuación. Ten en cuenta que puede haber alguna variación en la forma en que se presenta el resultado, dependiendo de la complejidad de la ecuación.

Si el resultado es una solución única, Mathematica te mostrará el valor de "x0" que satisface la ecuación. Si hay múltiples soluciones, Mathematica te mostrará todas las soluciones posibles.

También es importante tener en cuenta que si la ecuación no tiene una solución explícita para "x0", Mathematica te mostrará la ecuación en forma simbólica, lo que significa que el valor de "x0" dependerá de los otros parámetros de la ecuación.

Paso 4: Verificar la solución

Después de obtener el resultado de la ecuación, es recomendable verificar la solución encontrada. Puedes hacerlo sustituyendo el valor de "x0" obtenido en la ecuación original y comprobando si se satisface.

Por ejemplo, si la ecuación original es "2x0 + 3 = 7", y Mathematica te devuelve "x0 = 2", puedes sustituir ese valor en la ecuación y verificar si se cumple: "22 + 3 = 7". Si la igualdad es verdadera, entonces la solución encontrada es correcta.

Recuerda que Mathematica es una herramienta poderosa y versátil para resolver ecuaciones y despejar variables. Con los pasos anteriores, podrás despejar fácilmente la variable "x0" en tus ecuaciones y obtener resultados precisos y confiables.

Existen métodos alternativos para resolver ecuaciones en Mathematica

Si bien Mathematica es una poderosa herramienta para resolver ecuaciones, existen métodos alternativos que pueden facilitar el proceso de despejar x0. Uno de estos métodos es el uso de funciones de despeje específicas, como Solve o Reduce, que permiten encontrar la solución exacta de una ecuación. Estas funciones tienen la ventaja de brindar resultados precisos y completos, pero pueden ser más lentas en comparación con otros métodos.

Otra opción es utilizar métodos numéricos, como el método de Newton-Raphson o el método de bisección, que permiten aproximar la solución de una ecuación mediante iteraciones sucesivas. Estos métodos son especialmente útiles cuando la ecuación no puede resolverse de forma exacta o cuando se necesita una solución rápida. Sin embargo, es importante tener en cuenta que los resultados obtenidos pueden estar sujetos a cierto grado de error.

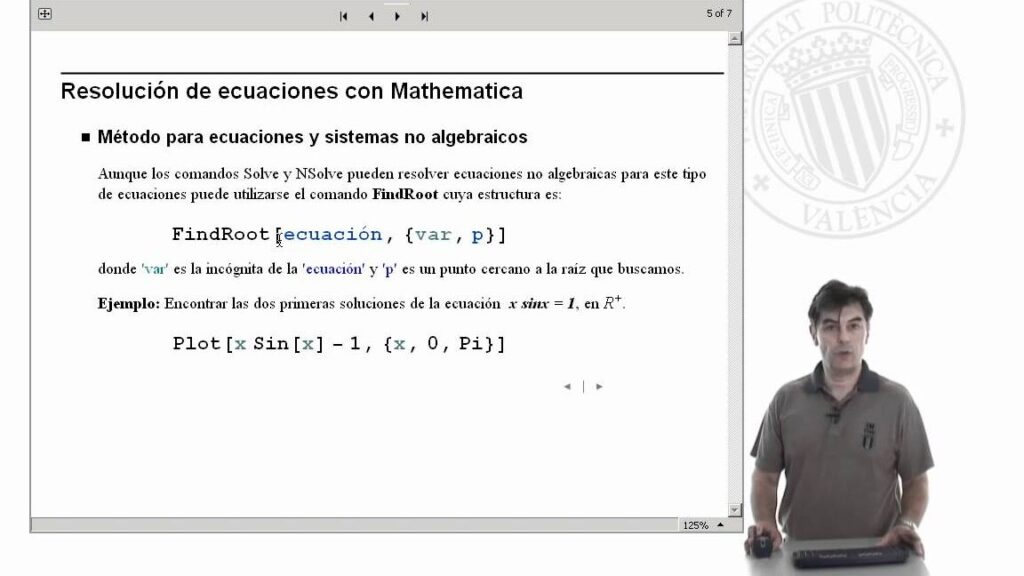
Además, existen paquetes y librerías adicionales disponibles en Mathematica que ofrecen una amplia gama de herramientas para resolver ecuaciones. Por ejemplo, el paquete NDSolve permite resolver ecuaciones diferenciales numéricas, mientras que el paquete FindRoot puede utilizarse para encontrar raíces de funciones. Estas herramientas adicionales son especialmente útiles cuando se trabaja con ecuaciones más complejas o cuando se requiere un mayor grado de precisión en los resultados.

Resolver ecuaciones en Mathematica puede hacerse de diferentes maneras, ya sea utilizando las funciones de despeje incorporadas, los métodos numéricos o las herramientas adicionales disponibles en paquetes y librerías. La elección del método dependerá de la naturaleza de la ecuación, la precisión requerida y el tiempo disponible para obtener los resultados. Experimentar con diferentes enfoques puede ayudar a encontrar la mejor solución para cada caso.

Qué funciones específicas de Mathematica son útiles para resolver ecuaciones

Existen varias funciones específicas en Mathematica que son útiles para resolver ecuaciones de forma sencilla. Una de las más utilizadas es la función "Solve", que permite encontrar las soluciones exactas de una ecuación. Por ejemplo, si se tiene una ecuación lineal como "2x + 3 = 7", se puede utilizar la función "Solve" para despejar la incógnita "x" y obtener la solución "x = 2".

Otra función muy útil es "NSolve", que se utiliza para resolver ecuaciones numéricas. Esta función encuentra las soluciones aproximadas de una ecuación, lo cual puede ser útil cuando las soluciones exactas son difíciles de obtener. Por ejemplo, si se tiene una ecuación cuadrática como "x^2 + 4x - 5 = 0", se puede utilizar la función "NSolve" para encontrar las soluciones aproximadas.

Además de estas funciones, también existen otras herramientas en Mathematica que pueden ser útiles para resolver ecuaciones. Por ejemplo, la función "Reduce" permite encontrar todas las soluciones de una ecuación en un rango determinado de valores. La función "DSolve" se utiliza para resolver ecuaciones diferenciales, mientras que la función "RSolve" se utiliza para resolver ecuaciones en recurrencia.

Cómo utilizar estas funciones en Mathematica

Para utilizar las funciones mencionadas anteriormente en Mathematica, es necesario seguir algunos pasos simples. Primero, se debe abrir el programa y crear una nueva celda de código. Luego, se puede escribir la ecuación que se desea resolver utilizando la notación adecuada.

Por ejemplo, si se desea resolver la ecuación cuadrática "x^2 + 4x - 5 = 0", se puede escribir en la celda de código lo siguiente:


Solve


Una vez que se ha escrito la ecuación, se puede ejecutar la celda de código haciendo clic en el botón de "Ejecutar" o presionando la tecla "Shift + Enter". Mathematica calculará las soluciones de la ecuación y las mostrará en el resultado.

Mathematica ofrece diversas funciones y herramientas que facilitan la resolución de ecuaciones de forma rápida y precisa. Ya sea que se necesite encontrar soluciones exactas o aproximadas, estas funciones son de gran utilidad para los usuarios de Mathematica.

Cómo puedo representar gráficamente las soluciones de una ecuación en Mathematica

Una de las ventajas de utilizar Mathematica es la capacidad de representar gráficamente las soluciones de una ecuación de forma rápida y sencilla. Para lograr esto, debemos seguir algunos pasos simples.

En primer lugar, necesitamos definir la ecuación que queremos resolver utilizando la función "Equal" en Mathematica. Por ejemplo, si queremos resolver la ecuación "x^2 - 4x + 3 == 0", debemos escribir:

eq = x^2 - 4x + 3 == 0;

A continuación, utilizamos la función "Solve" para encontrar las soluciones de la ecuación. Esta función devuelve una lista de reglas de la forma "x -> valor", donde "valor" representa una de las soluciones de la ecuación. Por ejemplo:

solutions = Solve;

Una vez que tenemos las soluciones, podemos utilizar la función "Plot" para graficarlas. Esta función toma como argumento una expresión y un rango de valores para la variable independiente. Por ejemplo, si queremos graficar las soluciones de la ecuación en el rango de x de -5 a 5, debemos escribir:

Plot;

Al ejecutar estas líneas de código, obtendremos una gráfica que representa las soluciones de la ecuación en el rango especificado. Esto nos permite visualizar de manera clara y concisa las soluciones y su comportamiento en el espacio real.

Para representar gráficamente las soluciones de una ecuación en Mathematica, debemos definir la ecuación, encontrar las soluciones utilizando la función "Solve" y, finalmente, graficar las soluciones utilizando la función "Plot". Esta capacidad de Mathematica nos proporciona una herramienta poderosa para analizar y comprender las soluciones de ecuaciones de manera visual.

Qué tipo de ecuaciones puedo resolver utilizando Mathematica

Mathematica es una poderosa herramienta que permite resolver una amplia variedad de ecuaciones matemáticas. Puedes utilizar Mathematica para resolver ecuaciones lineales, cuadráticas, cúbicas e incluso ecuaciones de orden superior. Además, también es posible resolver ecuaciones transcendentes, como las ecuaciones trigonométricas y exponenciales.

La flexibilidad de Mathematica te permite definir tus propias funciones y ecuaciones personalizadas, lo que significa que no estás limitado a los tipos de ecuaciones predefinidos. Esto hace que Mathematica sea una herramienta versátil para resolver problemas matemáticos de cualquier nivel de complejidad.

Independientemente del tipo de ecuación que necesites resolver, Mathematica te brinda la capacidad de obtener soluciones precisas y detalladas, lo que lo convierte en una herramienta invaluable para investigadores, estudiantes y profesionales de las matemáticas.

Cuáles son las limitaciones de Mathematica al resolver ecuaciones

Mathematica es una poderosa herramienta para resolver ecuaciones, pero como cualquier software, tiene sus limitaciones. Una de las limitaciones más comunes es la incapacidad de resolver ecuaciones con múltiples soluciones o soluciones complejas. También puede tener dificultades con ecuaciones que contienen funciones especiales o integrales. Además, Mathematica puede tener problemas para resolver ecuaciones cuando se le proporcionan valores iniciales no adecuados. Es importante tener en cuenta estas limitaciones al utilizar Mathematica para resolver ecuaciones y estar preparado para buscar soluciones alternativas cuando sea necesario.

Se puede resolver sistemas de ecuaciones con Mathematica? ¿Cómo se hace

¡Claro que sí! Mathematica es una poderosa herramienta para resolver sistemas de ecuaciones de una manera rápida y sencilla. A través de su lenguaje de programación y sus funciones integradas, Mathematica nos permite ingresar ecuaciones y obtener los valores de las incógnitas de forma automática.

Para resolver un sistema de ecuaciones en Mathematica, podemos utilizar la función Solve. Esta función nos permite especificar las ecuaciones que queremos resolver y las incógnitas que deseamos despejar. Por ejemplo, si tenemos el siguiente sistema de ecuaciones:

x + y = 5
2x - y = 1

Podemos resolverlo de la siguiente manera:

Solve

El resultado será una lista de reglas que nos indicarán los valores de las variables. En este caso, obtendríamos {x -> 2, y -> 3}, lo que significa que las soluciones del sistema de ecuaciones son x = 2 e y = 3.

De esta forma, con Mathematica podemos resolver sistemas de ecuaciones de manera eficiente y obtener los valores de las incógnitas de forma automática.

Existe alguna función en Mathematica para verificar si una solución de una ecuación es correcta

En Mathematica, puedes utilizar la función "Solve" para resolver ecuaciones algebraicas. Sin embargo, a veces es posible que desees verificar si la solución obtenida es correcta. Para eso, puedes utilizar la función "Simplify" para simplificar la ecuación original y luego evaluar si la solución satisface la ecuación simplificada.

Por ejemplo, supongamos que tienes la ecuación x^2 + 3x - 4 == 0 y encuentras que la solución es x = -4. Para verificar si esta solución es correcta, puedes simplificar la ecuación original utilizando Simplify y obtener x^2 + 3x - 4 == 0. Luego, evalúa si la solución x = -4 satisface esta ecuación simplificada. Si lo hace, entonces la solución es correcta.

Esta función de verificación es útil para asegurarte de que las soluciones que obtienes son válidas y no tienen errores en el proceso de resolución.

Se pueden resolver ecuaciones diferenciales en Mathematica? ¿Cómo se hace

Sí, es posible resolver ecuaciones diferenciales en Mathematica de una manera fácil y eficiente. Mathematica es un potente software de cálculo matemático que ofrece una amplia gama de herramientas para resolver este tipo de ecuaciones. La forma más básica de resolver una ecuación diferencial en Mathematica es utilizando la función DSolve, que encuentra una solución analítica a la ecuación.

La sintaxis de la función DSolve es bastante sencilla. Solo necesitas ingresar la ecuación diferencial junto con las condiciones iniciales y Mathematica encontrará la solución exacta. Por ejemplo, si tienes la siguiente ecuación diferencial:

y'' + y' + y == 0

y quieres encontrar la solución para y con las condiciones iniciales y == 1 y y' == 0, simplemente puedes escribir:

DSolve + y' + y == 0, y == 1, y' == 0}, y, x]

Mathematica devolverá la solución exacta de la ecuación diferencial en términos de funciones matemáticas conocidas, como por ejemplo:

y == E^(-x/2) (C Cos x)/2] + C Sin x)/2])

Donde C y C son constantes arbitrarias que dependen de las condiciones iniciales.

También es posible resolver ecuaciones diferenciales numéricamente utilizando la función NDSolve. Esta función discretiza la ecuación diferencial y encuentra una solución numérica a través de métodos numéricos avanzados.

Mathematica es una herramienta poderosa para resolver ecuaciones diferenciales, ya sea de forma analítica o numérica. Su sintaxis sencilla y sus métodos eficientes hacen que sea una opción ideal para estudiantes, profesionales y aficionados a las matemáticas.

Puedo resolver ecuaciones con restricciones en Mathematica

Resuelve ecuaciones con restricciones en Mathematica de forma sencilla y eficiente. Mathematica es un software de cálculo matemático que permite realizar operaciones complejas, como resolver ecuaciones con múltiples variables y condiciones.

Para resolver una ecuación con restricciones utilizando Mathematica, simplemente debes seguir algunos pasos. Primero, define la ecuación que deseas resolver y especifica las restricciones. Luego, utiliza la función Solve para obtener la solución.

Por ejemplo, supongamos que queremos resolver la ecuación x^2 + y^2 == 1 con la restricción x > 0. En Mathematica, escribiríamos:

Solve

Este código devuelve la solución de la ecuación con las restricciones especificadas. En este caso, obtendríamos dos soluciones: {{x -> 1, y -> 0}, {x -> 1, y -> 0}}.

Con Mathematica, resolver ecuaciones con restricciones se vuelve una tarea fácil y rápida. Puedes experimentar con diferentes ecuaciones y restricciones para obtener los resultados deseados.

Existen recursos en línea donde pueda aprender más sobre la resolución de ecuaciones en Mathematica

Si estás interesado en aprender más sobre cómo resolver ecuaciones en Mathematica, hay varios recursos en línea que pueden ayudarte a profundizar tus conocimientos. Uno de los mejores lugares para comenzar es el sitio web oficial de Mathematica, donde puedes encontrar una extensa documentación y tutoriales que te guiarán a través del proceso de resolución de ecuaciones.

Además, también puedes aprovechar los numerosos videos y tutoriales disponibles en plataformas como YouTube. Aquí, expertos en Mathematica comparten sus conocimientos y te brindan consejos útiles para resolver ecuaciones de manera eficiente y fácil.

Otra opción es unirse a foros y comunidades en línea dedicadas a la programación y al uso de Mathematica. Estas comunidades son un excelente lugar para hacer preguntas, encontrar soluciones a problemas específicos y aprender de otros usuarios que ya tienen experiencia en la resolución de ecuaciones en Mathematica.

Finalmente, no olvides explorar libros y cursos especializados en Mathematica. Estos recursos suelen ofrecer una cobertura más detallada y estructurada de la resolución de ecuaciones, lo que te ayudará a desarrollar una comprensión sólida de los conceptos fundamentales.

Cómo puedo aprovechar al máximo las capacidades de resolución de ecuaciones de Mathematica

Las capacidades de resolución de ecuaciones de Mathematica hacen que sea una herramienta invaluable para los matemáticos y científicos. Pero, ¿cómo podemos aprovechar al máximo estas capacidades para resolver nuestras ecuaciones de manera eficiente?

Primero, es importante comprender las diferentes opciones disponibles en Mathematica para resolver ecuaciones. Desde la función básica Solve hasta las opciones más avanzadas como NSolve y FindRoot, Mathematica nos ofrece una amplia variedad de métodos para abordar diferentes tipos de ecuaciones.

Además, podemos aprovechar las capacidades de simplificación algebraica de Mathematica utilizando la función Simplify. Esta función nos permite simplificar nuestras ecuaciones antes de resolverlas, lo que puede ahorrar tiempo y mejorar la precisión de los resultados.

Otra forma de aprovechar al máximo las capacidades de resolución de ecuaciones de Mathematica es utilizando las funciones de manejo de incógnitas, como Reduce y Eliminate. Estas funciones nos permiten despejar variables específicas o eliminar variables no deseadas de nuestras ecuaciones, lo que puede facilitar la resolución de sistemas de ecuaciones complejos.

Además, podemos utilizar las capacidades gráficas de Mathematica para visualizar las soluciones de nuestras ecuaciones. La función ContourPlot nos permite trazar las curvas de nivel de nuestras ecuaciones en un gráfico bidimensional, lo que puede ayudarnos a comprender mejor las soluciones y encontrar regiones de interés.

Por último, es importante recordar que Mathematica es una herramienta poderosa pero compleja, y puede llevar tiempo y práctica dominar completamente sus capacidades de resolución de ecuaciones. Sin embargo, con paciencia y perseverancia, podemos aprovechar al máximo estas capacidades y resolver ecuaciones de manera rápida y eficiente.

Preguntas frecuentes (FAQ)

1. ¿Puedo resolver cualquier tipo de ecuación con Mathematica?

Sí, Mathematica es capaz de resolver ecuaciones algebraicas, diferenciales y funciones trascendentales.

2. ¿Necesito tener conocimientos avanzados de programación para usar Mathematica?

No, Mathematica tiene una interfaz intuitiva que permite resolver ecuaciones de manera sencilla, sin necesidad de programar.

3. ¿Cuál es la precisión de las soluciones obtenidas con Mathematica?

Las soluciones obtenidas con Mathematica suelen tener una precisión de hasta 15 dígitos decimales.

4. ¿Puedo resolver sistemas de ecuaciones con Mathematica?

Sí, Mathematica permite resolver sistemas de ecuaciones algebraicas lineales y no lineales.

5. ¿Mathematica tiene alguna limitación en cuanto al tamaño de las ecuaciones que se pueden resolver?

Mathematica es capaz de resolver ecuaciones de tamaño ilimitado, aunque el tiempo de cálculo puede aumentar en ecuaciones muy grandes.