Multiplica matrices 2x2 y 2x1 en Mathematica: guía completa

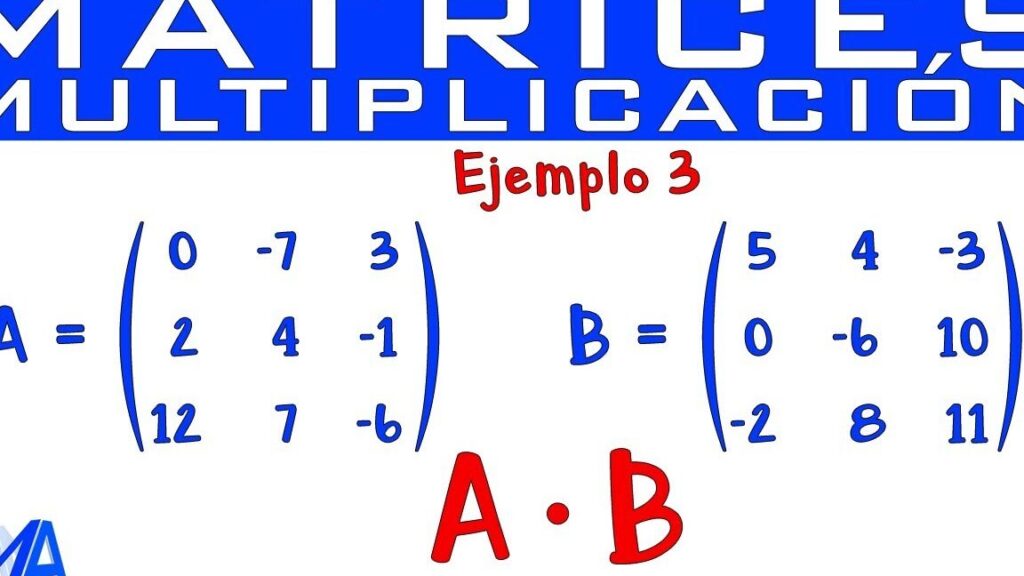
En el campo de la matemática y la programación, el cálculo de matrices es una herramienta esencial para resolver problemas numéricos y algebraicos. Una operación común es la multiplicación de matrices, que consiste en combinar dos matrices para obtener una tercera matriz resultante. En el caso específico de las matrices 2x2 y 2x1, es importante entender cómo se realiza esta multiplicación y cuál es su utilidad en diferentes áreas como la física, la ingeniería y las ciencias de la computación.

Exploraremos en detalle cómo multiplicar matrices 2x2 y 2x1 utilizando el software Mathematica. Empezaremos por explicar cómo se representa una matriz en Mathematica y cómo se realiza la multiplicación entre dos matrices. Luego, veremos ejemplos prácticos y aplicaciones de la multiplicación de matrices 2x2 y 2x1 en diferentes campos. Finalmente, proporcionaremos recursos y consejos útiles para aprovechar al máximo esta operación en Mathematica.

Cuál es la sintaxis correcta para multiplicar matrices de 2x2 y 2x1 en Mathematica

La multiplicación de matrices en Mathematica sigue una sintaxis específica para matrices de diferentes dimensiones. Para multiplicar una matriz 2x2 por una matriz 2x1, se utiliza el operador "Dot" o ".", seguido de las matrices a multiplicar.

Aquí hay un ejemplo de cómo se realiza la multiplicación:


matrizA = {{a, b}, {c, d}};
matrizB = {{x}, {y}};
resultado = matrizA . matrizB;
resultado


En este ejemplo, matrizA representa la matriz 2x2 y matrizB representa la matriz 2x1. El resultado de la multiplicación se guarda en la variable "resultado".

También puedes realizar la multiplicación directamente sin utilizar variables intermedias:


{{a, b}, {c, d}} . {{x}, {y}}


Este código producirá el mismo resultado que el ejemplo anterior.

Asegúrate de utilizar los corchetes dobles "{}" para definir las matrices y los corchetes simples "{}" para definir los elementos dentro de cada matriz. Esto es crucial para que Mathematica interprete correctamente la estructura de las matrices a multiplicar.

Recuerda también que la multiplicación de matrices solo es posible si el número de columnas de la matriz izquierda coincide con el número de filas de la matriz derecha.

Cuál es la diferencia entre la multiplicación de matrices y la multiplicación de elementos en Mathematica

En Mathematica, la multiplicación de matrices se realiza utilizando el operador ".dot", mientras que la multiplicación de elementos se realiza utilizando el operador "". La diferencia fundamental radica en el resultado obtenido. La multiplicación de matrices genera una nueva matriz cuyos elementos son el producto de las filas de la primera matriz por las columnas de la segunda matriz. En cambio, la multiplicación de elementos simplemente multiplica los elementos correspondientes de las dos matrices y genera una nueva matriz con los resultados. Es importante tener en cuenta esta diferencia para utilizar correctamente las operaciones de multiplicación en Mathematica.

Qué sucede si las dimensiones de las matrices no son compatibles para su multiplicación en Mathematica

En Mathematica, cuando intentamos multiplicar matrices de dimensiones no compatibles, se produce un error. Esto se debe a que la multiplicación de matrices requiere una correspondencia adecuada entre las dimensiones de las matrices. Específicamente, la cantidad de columnas de la primera matriz debe ser igual a la cantidad de filas de la segunda matriz.

Si las dimensiones no son compatibles, el programa arrojará un mensaje de error indicando que la multiplicación no se puede realizar. Esto es una medida de seguridad para asegurar que los cálculos sean correctos y evita resultados incorrectos o inesperados.

Es importante tener en cuenta las dimensiones de las matrices antes de intentar multiplicarlas en Mathematica, ya que la incompatibilidad de las dimensiones puede llevar a errores y resultados incorrectos.

Existen funciones predefinidas en Mathematica para multiplicar matrices de diferentes dimensiones

En Mathematica, existen diversas funciones predefinidas que permiten multiplicar matrices de diferentes dimensiones de forma sencilla y eficiente. Estas funciones son muy útiles para resolver problemas que involucran cálculos matriciales, como la resolución de sistemas de ecuaciones lineales o la transformación de coordenadas.

Una de las funciones más utilizadas para multiplicar matrices en Mathematica es la función Dot(). Esta función permite multiplicar dos matrices de la misma dimensión elemento a elemento, es decir, multiplicando los elementos correspondientes de cada matriz y sumándolos. La sintaxis de la función es la siguiente: Dot

Por ejemplo, supongamos que tenemos dos matrices de dimensiones 2x2 y 2x1, respectivamente. Para multiplicar estas matrices utilizando la función Dot(), simplemente debemos ingresar las matrices como argumentos de la función de la siguiente manera: Dot. El resultado será una nueva matriz de dimensiones 2x1.

Otra función útil para multiplicar matrices en Mathematica es la función Times(). Esta función permite multiplicar dos matrices de cualquier dimensión. La sintaxis de la función es la siguiente: Times. Al igual que con la función Dot(), simplemente debemos ingresar las matrices como argumentos de la función para obtener el resultado deseado.

Además de estas funciones predefinidas, Mathematica también ofrece la posibilidad de definir nuestras propias funciones para multiplicar matrices. Esto nos permite personalizar el proceso de multiplicación de matrices según nuestras necesidades específicas. Para definir una función de multiplicación de matrices personalizada, debemos utilizar la sintaxis adecuada y especificar las reglas de multiplicación que queremos aplicar.

Cuál es la importancia de la multiplicación de matrices en la resolución de problemas matemáticos y científicos

La multiplicación de matrices juega un papel fundamental en la resolución de problemas matemáticos y científicos. Permite combinar y relacionar diferentes conjuntos de datos y realizar cálculos complejos de una manera eficiente. Al multiplicar matrices, podemos obtener información más detallada sobre un sistema, como la solución de ecuaciones lineales o la representación de transformaciones geométricas. Además, es una herramienta esencial en áreas como la física, la economía y la informática. Dominar la multiplicación de matrices es fundamental para aquellos que buscan comprender y resolver problemas en estos campos. Por lo tanto, es importante aprender y practicar esta habilidad. ¡Veamos cómo multiplicar matrices 2x2 y 2x1 en Mathematica!

Qué técnicas o estrategias puedo utilizar para optimizar el tiempo de ejecución de la multiplicación de matrices en Mathematica

La multiplicación de matrices es una operación esencial en el ámbito de la programación y análisis de datos. En Mathematica, existen diversas técnicas y estrategias que se pueden utilizar para optimizar el tiempo de ejecución de esta operación.

1. Utilizar la función Dot

En Mathematica, la función Dot es la más eficiente para la multiplicación de matrices. Esta función utiliza algoritmos optimizados y procesamiento paralelo para realizar la operación en el menor tiempo posible.

2. Aprovechar las propiedades algebraicas

Al multiplicar matrices, es posible aprovechar propiedades algebraicas como la asociatividad y la distributividad para reducir la cantidad de operaciones necesarias. Esto puede agilizar significativamente el tiempo de ejecución.

3. Utilizar matrices de tipo Sparse

Si la matriz que estás multiplicando tiene muchos elementos nulos, puedes utilizar el tipo de dato Sparse en Mathematica. Este tipo de matriz almacena solo los elementos diferentes de cero, lo que reduce la cantidad de operaciones necesarias y acelera el cálculo.

4. Utilizar paralelismo

Mathematica cuenta con funciones y herramientas para aprovechar el paralelismo y utilizar múltiples núcleos de procesamiento al realizar cálculos intensivos como la multiplicación de matrices. Esto puede reducir significativamente el tiempo de ejecución.

5. Evitar bucles y utilizar operaciones vectorizadas

En Mathematica, evita utilizar bucles individuales para multiplicar matrices. En su lugar, aprovecha las operaciones vectorizadas que ya están optimizadas para trabajar con matrices de manera eficiente.

6. Utilizar matrices compactas

Si las matrices que estás multiplicando son de tamaño pequeño, considera utilizar matrices compactas en lugar de matrices regulares. Las matrices compactas son más eficientes en términos de uso de memoria y operaciones de cálculo.

7. Utilizar compilación just-in-time

Mathematica permite compilar funciones específicas para que se ejecuten de manera más rápida. Puedes utilizar la compilación just-in-time para la multiplicación de matrices y mejorar el rendimiento.

8. Realizar una preasignación de memoria

Antes de realizar la multiplicación de matrices, asigna la memoria necesaria para el resultado. Esto evita que se realicen asignaciones y liberaciones de memoria repetidas durante la ejecución, lo que puede ralentizar el proceso.

9. Experimentar con el tamaño de las matrices

Si bien las técnicas anteriores pueden ayudar a optimizar el tiempo de ejecución, también es importante considerar el tamaño de las matrices. Experimenta con matrices más pequeñas o fragmentos de matrices para evaluar el rendimiento y asegurarte de que estás obteniendo los resultados deseados en el menor tiempo posible.

Al multiplicar matrices en Mathematica, existen diversas estrategias y técnicas que puedes utilizar para optimizar el tiempo de ejecución. Desde utilizar la función Dot, aprovechar propiedades algebraicas, hasta utilizar paralelismo y matrices compactas, hay muchas opciones disponibles para acelerar el proceso y mejorar la eficiencia en tus cálculos.

Cuáles son algunos ejemplos prácticos donde la multiplicación de matrices de 2x2 y 2x1 en Mathematica es útil

La multiplicación de matrices de 2x2 y 2x1 en Mathematica tiene aplicaciones prácticas en diversos campos, como la física, la ingeniería y la economía. Por ejemplo, en física se puede utilizar para calcular el producto de un vector por una matriz de transformación, lo cual es útil para realizar transformaciones lineales en el espacio. En ingeniería, la multiplicación de matrices puede utilizarse en el diseño de sistemas de control o en el análisis de estructuras. En economía, puede aplicarse en la modelización de sistemas de ecuaciones lineales para analizar situaciones de oferta y demanda.

Uno de los ejemplos más comunes es el cálculo del producto de una matriz de rotación por un vector de posición en problemas de mecánica o robótica. Esto permite determinar la nueva posición de un objeto después de aplicar una rotación. Otro ejemplo es el cálculo de la transformación lineal de una imagen digital utilizando una matriz de coeficientes. Esto se utiliza en procesamiento de imágenes para aplicar efectos o correcciones a una imagen.

La multiplicación de matrices de 2x2 y 2x1 en Mathematica es útil en una amplia variedad de situaciones, desde la física y la ingeniería hasta la economía y el procesamiento de imágenes. Su capacidad para realizar cálculos matemáticos de manera eficiente y precisa la convierte en una herramienta poderosa para resolver problemas complejos.

Existen alternativas a Mathematica para realizar multiplicaciones de matrices de 2x2 y 2x1

Si bien Mathematica es una poderosa herramienta para realizar operaciones matemáticas, existen alternativas disponibles para aquellos que deseen multiplicar matrices de 2x2 y 2x1 sin utilizar este software. Una opción popular es utilizar lenguajes de programación como Python o MATLAB, que ofrecen bibliotecas y funciones que facilitan la multiplicación de matrices.

Python, por ejemplo, cuenta con la biblioteca NumPy, que proporciona una amplia gama de funciones para trabajar con matrices. Para multiplicar matrices 2x2 y 2x1 en Python utilizando NumPy, simplemente se deben crear los arrays correspondientes y utilizar la función dot().

En MATLAB, la multiplicación de matrices de 2x2 y 2x1 se puede realizar utilizando el operador o la función mtimes(). Ambas opciones ofrecen resultados precisos y eficientes.

Además de Python y MATLAB, también se pueden encontrar otras alternativas en línea, como calculadoras de matrices en sitios web especializados. Estas calculadoras permiten ingresar las matrices y realizar la multiplicación de forma rápida y sencilla, sin la necesidad de instalar software adicional.

Si bien Mathematica es una excelente opción para multiplicar matrices de 2x2 y 2x1, existen alternativas como Python, MATLAB y calculadoras en línea que pueden ser igualmente efectivas y convenientes para realizar este tipo de operaciones matemáticas.

Cómo puedo verificar si el resultado de la multiplicación de matrices en Mathematica es correcto

Para verificar si el resultado de la multiplicación de matrices en Mathematica es correcto, puedes seguir estos pasos:

Paso 1: Define las matrices

Comienza definiendo las matrices que deseas multiplicar. Por ejemplo, si tienes una matriz A de dimensiones 2x2 y una matriz B de dimensiones 2x1, puedes definirlas de la siguiente manera:

A = {{a11, a12}, {a21, a22}};
B = {{b1}, {b2}};

Paso 2: Realiza la multiplicación de matrices

Usa el operador de multiplicación de matrices en Mathematica para obtener el producto de A y B:

AB = A.B;

Paso 3: Calcula el resultado manualmente

Calcula manualmente el resultado de la multiplicación de A y B. Para ello, multiplica cada elemento de la primera fila de A por los elementos correspondientes de B, y luego suma los productos. Haz lo mismo para la segunda fila de A y los elementos de B.

Paso 4: Compara los resultados

Compara el resultado obtenido en el paso 2 (AB) con el resultado calculado manualmente. Si los resultados son iguales, entonces la multiplicación de matrices en Mathematica es correcta.

Recuerda que es importante verificar que las dimensiones de las matrices sean compatibles para la multiplicación, es decir, el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.

En caso de obtener resultados diferentes, revisa cuidadosamente los elementos de las matrices y los pasos que realizaste para identificar posibles errores.

Cuáles son los errores comunes que se cometen al multiplicar matrices en Mathematica y cómo evitarlos

Al multiplicar matrices en Mathematica, es común cometer algunos errores que pueden llevar a resultados incorrectos. Uno de los errores más comunes es olvidar verificar las dimensiones de las matrices antes de intentar multiplicarlas. Si las dimensiones no coinciden, obtendrás un error.

Otro error común es no tener en cuenta la diferencia entre multiplicar una matriz 2x2 por una matriz 2x1 y multiplicar una matriz 2x1 por una matriz 2x2. En el primer caso, obtendrás una matriz 2x1 como resultado, mientras que en el segundo caso, obtendrás una matriz 1x2.

Es importante recordar que la multiplicación de matrices en Mathematica se realiza utilizando el operador ".". Por ejemplo, para multiplicar una matriz A de dimensiones 2x2 por una matriz B de dimensiones 2x1, debes escribir A.B.

Si quieres evitar estos errores comunes, te recomiendo siempre verificar las dimensiones de las matrices y recordar el orden correcto de multiplicación. Además, es útil utilizar la función Dimensions para verificar las dimensiones de las matrices antes de multiplicarlas.

Existen funciones o paquetes complementarios en Mathematica que faciliten la multiplicación de matrices de 2x2 y 2x1

Sí, en Mathematica existen diversas funciones y paquetes que pueden facilitar la multiplicación de matrices de 2x2 y 2x1. Uno de ellos es el paquete "LinearAlgebra`MatrixManipulation`", que proporciona una amplia gama de operaciones y funciones relacionadas con matrices.

Para utilizar la función de multiplicación de matrices, simplemente debes cargar el paquete utilizando el comando: Needs. A partir de ahí, puedes utilizar la función MatrixMultiply para multiplicar matrices 2x2 y 2x1.

Por ejemplo, si tienes una matriz de 2x2 llamada A y una matriz de 2x1 llamada B, puedes multiplicarlas utilizando la siguiente sintaxis:

MatrixMultiply

Esto te dará la matriz resultante de la multiplicación de A y B.

También puedes utilizar la función Dot para lograr el mismo resultado. La sintaxis sería la siguiente:

A.B

Ambas funciones son equivalentes y te proporcionarán el resultado deseado.

Ten en cuenta que, para realizar estas operaciones, es importante que las dimensiones de las matrices sean compatibles. En el caso de la multiplicación de matrices 2x2 y 2x1, la matriz 2x2 debe tener 2 columnas y la matriz 2x1 debe tener 2 filas.

Además de estas funciones, también puedes utilizar operaciones algebraicas como la transposición de matrices y la inversión de matrices para realizar operaciones más avanzadas. El paquete "LinearAlgebra`MatrixManipulation`" proporciona diversas funciones para esto.

Espero que esta guía te sea útil para multiplicar matrices de 2x2 y 2x1 en Mathematica. ¡Prueba estas funciones y descubre cómo pueden facilitar tus cálculos matriciales!

Cuál es la complejidad computacional de la multiplicación de matrices en Mathematica y cómo afecta el rendimiento del sistema

La multiplicación de matrices es una operación fundamental en el ámbito de la informática y las matemáticas. En el caso de Mathematica, es esencial comprender la complejidad computacional de esta operación y cómo puede afectar el rendimiento del sistema.

La complejidad computacional de la multiplicación de matrices en Mathematica depende del tamaño de las matrices involucradas. En el caso de matrices 2x2 y 2x1, el cálculo se realiza de manera eficiente, ya que las dimensiones son pequeñas. Sin embargo, a medida que las matrices crecen en tamaño, el tiempo de ejecución aumenta considerablemente.

Es importante tener en cuenta que la multiplicación de matrices en Mathematica se basa en algoritmos y técnicas altamente optimizadas. Esto significa que el rendimiento del sistema puede variar dependiendo de la versión de Mathematica utilizada y del hardware del ordenador.

En general, se recomienda utilizar matrices pequeñas siempre que sea posible para minimizar el tiempo de cálculo. Además, es importante tener en cuenta que la complejidad computacional de la multiplicación de matrices puede aumentar exponencialmente a medida que se agregan más dimensiones a las matrices.

La multiplicación de matrices en Mathematica puede tener un impacto significativo en el rendimiento del sistema, especialmente cuando se trabajan con matrices de gran tamaño. Es importante comprender la complejidad computacional de esta operación y utilizar técnicas de optimización cuando sea necesario.

Preguntas frecuentes (FAQ)

1. ¿Puedo usar esta guía para multiplicar matrices de otros tamaños?

Esta guía está específicamente diseñada para multiplicar matrices de tamaño 2x2 y 2x1 en Mathematica. Si deseas multiplicar matrices de diferentes dimensiones, es posible que necesites ajustar el código y los pasos proporcionados en esta guía.

2. ¿Cuál es la importancia de multiplicar matrices 2x2 y 2x1?

Multiplicar matrices de tamaño 2x2 y 2x1 es útil en muchas aplicaciones, como en el análisis de sistemas lineales y en la resolución de ecuaciones lineales. Esta operación es especialmente relevante en la geometría y la física.

3. ¿Es posible multiplicar matrices de otros tipos en Mathematica?

Sí, Mathematica es una herramienta muy versátil para trabajar con matrices de diferentes tipos y tamaños. Puedes multiplicar matrices de cualquier dimensión utilizando las funciones y comandos adecuados en Mathematica.

4. ¿Cuáles son los pasos básicos para multiplicar matrices 2x2 y 2x1 en Mathematica?

Los pasos básicos para multiplicar matrices 2x2 y 2x1 en Mathematica incluyen definir las matrices, utilizar el operador ".dot" para multiplicarlas y mostrar el resultado mediante la función "Print".

5. ¿Qué otras operaciones matemáticas puedo realizar en Mathematica?

Mathematica es una herramienta poderosa que permite realizar una amplia gama de operaciones matemáticas, como cálculo diferencial e integral, manipulación simbólica, generación de gráficos y visualización de datos, entre muchas otras.