Manipula matrices fácilmente en Wolfram Mathematica: aprende cómo aquí

Wolfram Mathematica es un potente software de matemáticas utilizado por científicos, ingenieros y estudiantes en todo el mundo. Su amplia gama de funcionalidades permite realizar cálculos complejos, resolver ecuaciones y graficar datos, entre muchas otras cosas. Una de las características más importantes de Mathematica es su capacidad para manipular matrices de manera eficiente y precisa.

Exploraremos las diferentes operaciones que se pueden realizar con matrices en Mathematica. Aprenderemos cómo crear matrices, tanto manualmente como a partir de datos, cómo realizar operaciones básicas como suma, resta y multiplicación, y cómo acceder a elementos específicos de una matriz. Además, también veremos algunas funciones útiles para la manipulación y transformación de matrices, como la transposición, la inversión y la diagonalización.

Cuáles son las ventajas de utilizar Wolfram Mathematica para manipular matrices

Wolfram Mathematica es una poderosa herramienta que ofrece una amplia gama de funciones para manipular matrices de manera eficiente y fácil. Una de las principales ventajas de usar Mathematica es su capacidad para manejar matrices de cualquier tamaño, ya sean pequeñas o extremadamente grandes. Esto es especialmente útil cuando se trabaja con conjuntos de datos complejos o al realizar cálculos matemáticos avanzados.

Otra ventaja es la gran cantidad de operaciones matemáticas que se pueden realizar con matrices en Mathematica. Puedes sumar, restar, multiplicar, dividir y elevar matrices con facilidad. Además, Mathematica ofrece una amplia gama de funciones predefinidas para manipular matrices, como la transposición, la inversión y la diagonalización.

La sintaxis clara y concisa de Mathematica también hace que la manipulación de matrices sea más fácil. Puedes definir matrices utilizando una notación muy intuitiva y acceder a sus elementos utilizando índices claros y sencillos. Esto permite un código más legible y menos propenso a errores.

Otra ventaja importante es la capacidad de Mathematica para realizar cálculos simbólicos con matrices. Esto significa que puedes trabajar con variables simbólicas en lugar de números concretos, lo que resulta especialmente útil en problemas de álgebra lineal y cálculo matricial. Puedes realizar operaciones algebraicas, derivadas e integrales con matrices simbólicas, lo que abre un abanico de posibilidades para la resolución de ecuaciones y sistemas de ecuaciones lineales.

Por último, pero no menos importante, Mathematica también ofrece una amplia variedad de herramientas de visualización para matrices. Puedes representar matrices con gráficos vectoriales, mapas de calor, diagramas de dispersión y mucho más. Esto facilita la comprensión y visualización de los datos contenidos en las matrices.

Wolfram Mathematica es una poderosa herramienta que ofrece numerosas ventajas para la manipulación de matrices. Su capacidad para manejar matrices de cualquier tamaño, sus numerosas funciones predefinidas, su sintaxis clara y concisa, su capacidad para realizar cálculos simbólicos y sus herramientas de visualización hacen de Mathematica la elección ideal para aquellos que trabajan con matrices de manera regular.

Cómo puedo crear y definir una matriz en Wolfram Mathematica

Crear y definir una matriz en Wolfram Mathematica es muy sencillo. Puedes utilizar la función "Array" para crear una matriz vacía con dimensiones específicas. Por ejemplo, si quieres crear una matriz de 3x3, puedes escribir:

matriz = Array

Esto creará una matriz de 3 filas y 3 columnas, inicializada con ceros. Si deseas definir los valores de la matriz directamente, puedes hacerlo utilizando las llaves y separando los elementos por comas. Por ejemplo:

matriz = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}

Esto creará una matriz con los valores especificados. Ahora que sabes cómo crear y definir matrices en Wolfram Mathematica, ¡puedes empezar a manipularlas!

Existen funciones predefinidas en Wolfram Mathematica para realizar operaciones matriciales

Wolfram Mathematica es una poderosa herramienta para realizar cálculos matemáticos y manipular matrices de manera fácil y eficiente. Una de las principales ventajas de Mathematica es que ofrece una amplia variedad de funciones predefinidas para realizar operaciones matriciales sin tener que escribir código complicado desde cero.

Con Mathematica, puedes realizar operaciones básicas como suma, resta, multiplicación y división de matrices de manera muy sencilla. También puedes calcular la transpuesta de una matriz, encontrar la matriz inversa, calcular el determinante y mucho más. Estas funciones predefinidas te permiten ahorrar tiempo y esfuerzo, ya que no tienes que escribir algoritmos complejos para realizar estas operaciones.

Incluso puedes realizar operaciones más avanzadas, como la descomposición en valores singulares, la descomposición LU y la descomposición de Cholesky. Estas operaciones son esenciales en el ámbito de la estadística y el análisis numérico, y Mathematica simplifica enormemente su implementación.

Además de las operaciones matriciales básicas, Mathematica también ofrece una amplia gama de funciones para manipular vectores y realizar operaciones vectoriales. Puedes sumar y restar vectores, calcular el producto escalar y el producto cruz, encontrar la magnitud y dirección de un vector, entre otras muchas operaciones.

No importa si eres un principiante en el ámbito de las matemáticas o si eres un experto en programación, Mathematica te brinda todas las herramientas necesarias para manipular matrices y vectores de manera eficiente y precisa. Aprovecha estas funciones predefinidas y simplifica tus cálculos matriciales con Wolfram Mathematica.

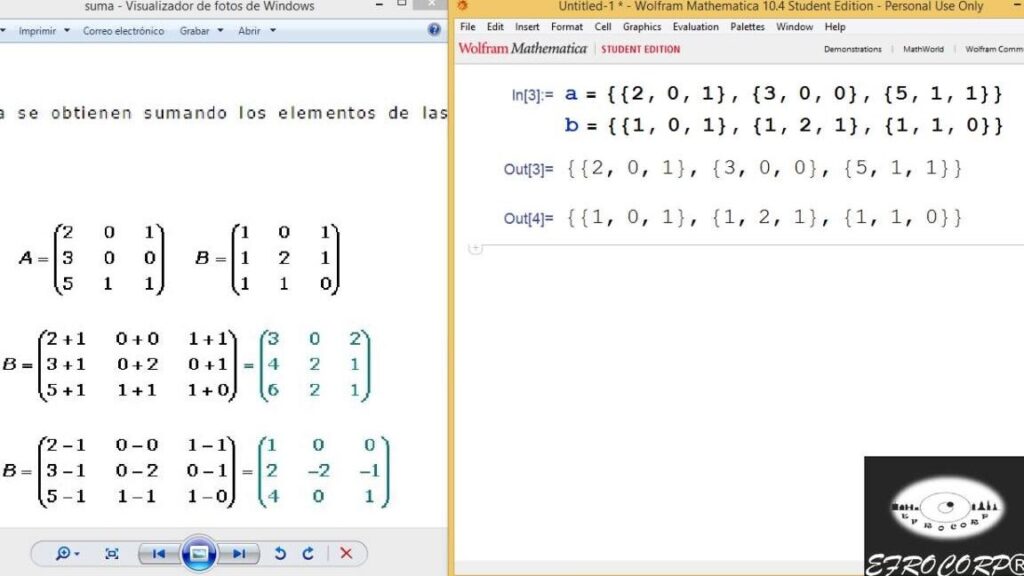
Cuál es la sintaxis para sumar dos matrices en Wolfram Mathematica

La sintaxis para sumar dos matrices en Wolfram Mathematica es muy sencilla. Para sumar dos matrices A y B, simplemente utilizamos el operador "+". Por ejemplo, si tenemos la matriz A = {{1, 2, 3}, {4, 5, 6}} y la matriz B = {{7, 8, 9}, {10, 11, 12}}, podemos sumarlas de la siguiente manera: A + B. El resultado será la matriz C = {{8, 10, 12}, {14, 16, 18}}. Es importante tener en cuenta que las matrices deben tener las mismas dimensiones para poder sumarse correctamente.

Además de la suma de matrices, en Wolfram Mathematica también podemos realizar otras operaciones con matrices, como la resta, la multiplicación, la transposición y la inversión. Estas operaciones se realizan de manera similar utilizando los operadores correspondientes.

Por ejemplo, para restar dos matrices A y B, utilizamos el operador "-". Si tenemos la matriz A = {{1, 2}, {3, 4}} y la matriz B = {{5, 6}, {7, 8}}, podemos restarlas de la siguiente manera: A - B. El resultado será la matriz C = {{-4, -4}, {-4, -4}}.

Para multiplicar dos matrices A y B, utilizamos el operador ".". Si tenemos la matriz A = {{1, 2}, {3, 4}} y la matriz B = {{5, 6}, {7, 8}}, podemos multiplicarlas de la siguiente manera: A.B. Sin embargo, es importante tener en cuenta que para que la multiplicación de matrices sea válida, el número de columnas de la matriz A debe ser igual al número de filas de la matriz B.

La transposición de una matriz se realiza utilizando el operador "Transpose". Por ejemplo, si tenemos la matriz A = {{1, 2, 3}, {4, 5, 6}}, podemos obtener su transpuesta de la siguiente manera: Transpose. El resultado será la matriz transpuesta B = {{1, 4}, {2, 5}, {3, 6}}.

La inversión de una matriz se realiza utilizando el operador "Inverse". Por ejemplo, si tenemos la matriz A = {{1, 2}, {3, 4}}, podemos obtener su inversa de la siguiente manera: Inverse. Sin embargo, es importante tener en cuenta que no todas las matrices son invertibles. Una matriz solo es invertible si su determinante es diferente de cero.

Wolfram Mathematica ofrece una amplia gama de funcionalidades para manipular matrices de manera fácil y eficiente. Con su sintaxis sencilla y poderosas herramientas, podemos realizar operaciones básicas como la suma y la resta, así como operaciones más avanzadas como la multiplicación, la transposición y la inversión de matrices.

Cómo puedo multiplicar una matriz por un escalar en Wolfram Mathematica

En Wolfram Mathematica, puedes multiplicar una matriz por un escalar utilizando la función "Times". Primero, define la matriz utilizando la notación de llaves, por ejemplo, A = {{1, 2}, {3, 4}}. Luego, para multiplicar la matriz A por un escalar k, simplemente escribe k A. Esto multiplicará cada elemento de la matriz por el escalar k.

Por ejemplo, si quieres multiplicar la matriz A por 2, escribe 2 A. Esto resultaría en la matriz {{2, 4}, {6, 8}}. De manera similar, si deseas multiplicar la matriz A por -1, escribe -1 A para obtener la matriz negativa de A.

Recuerda que para que la multiplicación por un escalar funcione correctamente, la matriz debe ser numérica y tener dimensiones compatibles con la operación.

Qué métodos existen en Wolfram Mathematica para calcular la inversa de una matriz

En Wolfram Mathematica, existen varios métodos que puedes utilizar para calcular la inversa de una matriz. Uno de los métodos más comunes es utilizar la función "Inverse". Por ejemplo, si tienes una matriz A, puedes calcular su inversa utilizando el siguiente código:

Inverse

Este código devolverá la matriz inversa de A. Sin embargo, ten en cuenta que la función "Inverse" solo puede calcular la inversa de matrices cuadradas no singulares.

Otro método que puedes utilizar es el método de eliminación de Gauss-Jordan. Este método implica realizar operaciones elementales en las filas de la matriz hasta obtener una matriz identidad en el lado izquierdo y la matriz inversa en el lado derecho.

Además, también puedes utilizar el método de descomposición LU (Lower-Upper) para calcular la inversa de una matriz. Este método implica descomponer la matriz original en dos matrices, una matriz triangular inferior L y una matriz triangular superior U. Luego, puedes utilizar estas matrices para calcular la inversa de la matriz original.

Estos son solo algunos de los métodos disponibles en Wolfram Mathematica para calcular la inversa de una matriz. Dependiendo de tus necesidades y de las propiedades de la matriz, puedes elegir el método que mejor se adapte a tu situación.

Cuáles son las funciones más útiles para obtener información y propiedades de una matriz en Wolfram Mathematica

En este artículo, te enseñaremos algunas de las funciones más útiles en Wolfram Mathematica para obtener información y propiedades de una matriz. Además de las operaciones básicas de manipulación de matrices, Mathematica proporciona una amplia gama de funciones que te permiten realizar tareas más avanzadas.

Una de las funciones más útiles es la función Dimensions, que te permite obtener las dimensiones de una matriz en términos de filas y columnas. Esto es especialmente útil cuando estás trabajando con matrices de diferentes tamaños y necesitas asegurarte de que sean compatibles para realizar operaciones.

Otra función útil es Transpose, que te permite intercambiar las filas y columnas de una matriz. Esto es útil cuando necesitas realizar cálculos o análisis que requieren una orientación diferente de los datos en la matriz.

Además de estas funciones básicas, Mathematica también proporciona funciones para calcular determinantes, autovalores y autovectores de una matriz. Estas funciones son muy útiles en álgebra lineal y te permiten obtener información importante sobre las propiedades de una matriz.

Wolfram Mathematica ofrece una amplia gama de funciones para manipular y analizar matrices. Ya sea que necesites obtener información sobre las dimensiones de una matriz, transponerla o calcular sus propiedades, Mathematica tiene las herramientas que necesitas para hacerlo de manera rápida y sencilla.

Qué técnicas puedo utilizar en Wolfram Mathematica para calcular los autovalores y autovectores de una matriz

En Wolfram Mathematica, dispones de diversas técnicas que te permiten calcular los autovalores y autovectores de una matriz de manera sencilla. Una opción es utilizar la función Eigensystem, que te devuelve tanto los autovalores como los autovectores de la matriz especificada. También puedes utilizar la función Eigenvalues para obtener solo los autovalores y luego utilizar la función Eigenvectors para obtener los autovectores correspondientes. Otra alternativa es utilizar la función CharacteristicPolynomial para calcular el polinomio característico de la matriz y luego resolverlo para obtener los autovalores.

Además, es importante mencionar que Mathematica también ofrece la posibilidad de trabajar con matrices simbólicas, lo que te permitirá realizar cálculos con matrices genéricas. Esto resulta especialmente útil en casos donde no conoces los valores concretos de los elementos de la matriz. Para trabajar con matrices simbólicas, puedes utilizar los comandos SymbolicMatrix y SymbolicVariable.

¿Cómo puedo utilizar estas técnicas en Mathematica?

Para calcular los autovalores y autovectores de una matriz en Mathematica, simplemente debes seguir los siguientes pasos:

1. Define la matriz que deseas analizar.
2. Utiliza la función Eigensystem para obtener tanto los autovalores como los autovectores de la matriz. Por ejemplo, si tu matriz se llama "A", puedes escribir la siguiente línea de código: eig = Eigensystem;
3. Si solo te interesan los autovalores, utiliza la función Eigenvalues en lugar de Eigensystem. Por ejemplo, si quieres obtener únicamente los autovalores de la matriz "A", puedes escribir la siguiente línea de código: autovalores = Eigenvalues;
4. Si deseas obtener únicamente los autovectores, utiliza la función Eigenvectors en lugar de Eigensystem. Por ejemplo, si quieres obtener solo los autovectores correspondientes a la matriz "A", puedes escribir la siguiente línea de código: autovectores = Eigenvectors;

Recuerda que Mathematica te permite realizar operaciones matemáticas tanto con matrices numéricas como simbólicas. Esto te brinda una gran flexibilidad a la hora de trabajar con matrices y facilita enormemente el cálculo de autovalores y autovectores.

Es posible resolver sistemas de ecuaciones lineales utilizando matrices en Wolfram Mathematica

Resolver sistemas de ecuaciones lineales puede ser una tarea complicada, pero gracias a Wolfram Mathematica, este proceso se vuelve mucho más sencillo. En Mathematica, las matrices son una herramienta poderosa que te permiten organizar y manipular datos de una manera eficiente. Con algunas líneas de código, puedes crear una matriz, realizar operaciones matemáticas con ella y obtener soluciones precisas a sistemas de ecuaciones lineales.

Para crear una matriz en Mathematica, simplemente utilizamos la función MatrixForm seguida de los elementos que deseamos ingresar. Por ejemplo, si queremos crear una matriz 2x2 con los elementos 1, 2, 3 y 4, escribiríamos:

MatrixForm

Esto nos mostraría la matriz en una forma visualmente agradable. Sin embargo, si queremos realizar operaciones matemáticas con la matriz, necesitamos asignarla a una variable. Por ejemplo:

A = {{1, 2}, {3, 4}};

Ahora podemos realizar diferentes operaciones matemáticas con la matriz A. Por ejemplo, si queremos encontrar su inversa, simplemente escribimos:

Inverse

Esto nos daría la matriz inversa de A. Podemos usar esta información para resolver sistemas de ecuaciones lineales. Por ejemplo, si tenemos el sistema de ecuaciones:

2x + 3y = 10

4x + 5y = 20

Podemos representarlo en forma matricial como:

A = {{2, 3}, {4, 5}};

b = {{10}, {20}};

Para encontrar la solución, simplemente necesitamos multiplicar la matriz inversa de A por la matriz b. En Mathematica, esto se hace utilizando el signo de multiplicación . Por ejemplo:

x = Inverse  b;

La variable x ahora tiene la solución del sistema de ecuaciones lineales. Si queremos obtener los valores de x y y, simplemente escribimos:

x]
y = x];

Esto nos daría los valores de x y y respectivamente. Así de fácil es resolver sistemas de ecuaciones lineales utilizando matrices en Wolfram Mathematica.

Cómo puedo graficar una matriz en Wolfram Mathematica y visualizar su estructura y valores

Graficar una matriz en Wolfram Mathematica es muy sencillo. Para visualizar su estructura y valores, puedes utilizar la función ArrayPlot. Esta función te permite representar cada elemento de la matriz como un píxel o un punto en un plano cartesiano. Así, podrás identificar fácilmente patrones o características específicas de la matriz.

Para utilizar ArrayPlot, simplemente debes ingresar la matriz como argumento de la función. Por ejemplo, si tienes una matriz llamada mat, puedes graficarla utilizando el siguiente código:

ArrayPlot

Al ejecutar este código, Mathematica generará una representación gráfica de la matriz mat. Cada elemento de la matriz se visualizará como un píxel o punto de color, y la posición de cada elemento en la matriz se mantendrá en la representación gráfica.

Existen recursos adicionales, como tutoriales o cursos, para aprender más sobre la manipulación de matrices en Wolfram Mathematica

Si quieres profundizar tus conocimientos sobre la manipulación de matrices en Wolfram Mathematica, tienes a tu disposición diversos recursos adicionales que pueden ayudarte en tu aprendizaje.

Una opción recomendada es buscar tutoriales en línea que se enfoquen en la manipulación de matrices en Wolfram Mathematica. Estos tutoriales te permitirán seguir paso a paso ejemplos prácticos que te ayudarán a comprender mejor cómo utilizar las diferentes funciones y comandos disponibles en el software.

Otra alternativa es inscribirte en cursos especializados en Wolfram Mathematica, que se enfoquen específicamente en la manipulación de matrices. Estos cursos suelen ser impartidos por expertos en la materia y te brindarán una formación más profunda y completa sobre este tema.

Además, puedes consultar la documentación oficial de Wolfram Mathematica, donde encontrarás información detallada sobre todas las funciones y comandos relacionados con la manipulación de matrices. Esta documentación suele estar actualizada y te proporcionará ejemplos prácticos que podrás seguir para mejorar tus habilidades en este ámbito.

Preguntas frecuentes (FAQ)

1. ¿Qué es Wolfram Mathematica?

Wolfram Mathematica es un software de matemáticas desarrollado por Wolfram Research. Permite realizar cálculos, visualizar datos, manipular matrices y resolver problemas matemáticos de manera fácil y eficiente.

2. ¿Qué ventajas tiene usar Wolfram Mathematica para manipular matrices?

Wolfram Mathematica ofrece una amplia gama de funciones y herramientas específicas para manipular matrices, lo que facilita enormemente el trabajo con este tipo de estructuras de datos. Además, cuenta con una sintaxis intuitiva y potentes capacidades de visualización.

3. ¿Puedo realizar operaciones matemáticas básicas con matrices en Wolfram Mathematica?

Sí, Wolfram Mathematica permite realizar todas las operaciones matemáticas básicas con matrices, como suma, resta, multiplicación, transposición, inversión, entre otras. Además, ofrece funciones específicas para realizar operaciones más complejas, como la eliminación de Gauss-Jordan y la descomposición LU.

4. ¿Puedo importar y exportar matrices desde y hacia otras aplicaciones en Wolfram Mathematica?

Sí, Wolfram Mathematica cuenta con funciones para importar y exportar matrices desde y hacia otros formatos y aplicaciones, como CSV, Excel, Matlab, entre otros. Esto facilita la integración con otras herramientas y permite el intercambio de datos de manera sencilla.

5. ¿Se requieren conocimientos avanzados de programación para trabajar con matrices en Wolfram Mathematica?

No necesariamente. Si bien tener conocimientos de programación puede ser útil para aprovechar al máximo las capacidades de Wolfram Mathematica, la manipulación básica de matrices se puede realizar utilizando la interfaz gráfica y las funciones predefinidas del software. Sin embargo, aprender a programar en Wolfram Language puede potenciar enormemente la manipulación y análisis de matrices.