Integración por Monte Carlo en Mathematica: guía paso a paso

La integración por Monte Carlo es un método numérico utilizado para estimar el valor de una integral a través de la generación aleatoria de puntos en el espacio. Este enfoque es particularmente útil en casos en los que la integración analítica es difícil o imposible de realizar. Mathematica, un popular software de matemáticas, ofrece una amplia gama de herramientas y funciones para llevar a cabo la integración por Monte Carlo de manera eficiente y precisa.

Te guiaré paso a paso a través del proceso de realizar una integración por Monte Carlo en Mathematica. Veremos cómo generar puntos aleatorios, cómo definir la función a integrar, cómo calcular el valor estimado de la integral y cómo mejorar la precisión utilizando técnicas como el muestreo estratificado y la reducción de la varianza. Además, exploraremos algunas aplicaciones prácticas de la integración por Monte Carlo en áreas como la física, la economía y la estadística.

Qué es la integración por Monte Carlo y cómo funciona en Mathematica

La integración por Monte Carlo es un método numérico utilizado para calcular aproximaciones de integrales definidas. A diferencia de otros métodos, como la regla del trapecio o la regla de Simpson, la integración por Monte Carlo se basa en el uso de números aleatorios para estimar el valor de la integral.

En Mathematica, este proceso se realiza utilizando la función NIntegrate con la opción Method->"MonteCarlo". Al especificar la función a integrar, los límites de integración y el número de puntos a generar, Mathematica utiliza el método de Monte Carlo para calcular la aproximación de la integral.

Paso 1: Definir la función a integrar

El primer paso para realizar una integración por Monte Carlo en Mathematica es definir la función que queremos integrar. Podemos usar tanto funciones predefinidas en Mathematica como funciones definidas por el usuario. Por ejemplo, si queremos calcular la integral de f(x) = x^2 en el intervalo , podemos definir la función de la siguiente manera:

f := x^2

Paso 2: Especificar los límites de integración

Una vez que tenemos definida la función a integrar, el siguiente paso es especificar los límites de integración. En el ejemplo anterior, los límites de integración son . Podemos hacerlo de la siguiente manera:

limiteInferior = 0;
limiteSuperior = 1;

Paso 3: Generar los puntos aleatorios

El siguiente paso es generar el número de puntos aleatorios que se utilizarán en el cálculo de la integral. Cuantos más puntos generemos, mayor será la precisión de la aproximación. En Mathematica, podemos generar los puntos aleatorios utilizando la función RandomReal. Por ejemplo, si queremos generar 1000 puntos aleatorios en el intervalo , podemos hacerlo de la siguiente manera:

puntosAleatorios = RandomReal;

Paso 4: Calcular la aproximación de la integral

Una vez que tenemos los puntos aleatorios generados, podemos utilizar la función NIntegrate con la opción Method->"MonteCarlo" para calcular la aproximación de la integral. En el ejemplo anterior, podemos hacerlo de la siguiente manera:

aproximacionIntegral = NIntegrate, {x, limiteInferior, limiteSuperior}, Method -> "MonteCarlo"];

Paso 5: Mostrar el resultado

Finalmente, podemos mostrar el resultado de la aproximación de la integral utilizando la función Print. Por ejemplo, podemos hacerlo de la siguiente manera:

Print;

Este es el proceso básico para realizar una integración por Monte Carlo en Mathematica. Recuerda que la precisión de la aproximación dependerá del número de puntos aleatorios que generes. Cuantos más puntos, mayor será la precisión, pero también mayor será el tiempo de cálculo.

Cuál es la ventaja de utilizar la integración por Monte Carlo en comparación con otros métodos de integración

La integración por Monte Carlo es un método numérico que utiliza números aleatorios para aproximar el valor de una integral. A diferencia de otros métodos de integración, como el método de Riemann o los métodos de cuadratura, la integración por Monte Carlo tiene varias ventajas.

Una de las ventajas clave es su capacidad para manejar integrales de mayor dimensión. Mientras que otros métodos pueden volverse extremadamente complejos y difíciles de implementar en dimensiones superiores, la integración por Monte Carlo sigue siendo una opción factible. Esto se debe a que el método no depende de particionar el espacio de integración, lo que reduce el tiempo y la complejidad computacional.

Además, la integración por Monte Carlo es especialmente útil cuando la función a integrar es de difícil evaluación analítica o cuando no se conoce una fórmula cerrada. En estos casos, el método proporciona una aproximación numérica precisa y flexible.

Otra ventaja importante es su capacidad para manejar funciones con singularidades o discontinuidades. A diferencia de otros métodos de integración, que pueden tener dificultades para lidiar con estas características, la integración por Monte Carlo puede manejarlas sin problemas. Esto se debe a que el método no requiere una partición específica del dominio de integración, lo que permite que los puntos de muestreo se distribuyan libremente.

La integración por Monte Carlo ofrece varias ventajas clave en comparación con otros métodos de integración. Su capacidad para manejar integrales de mayor dimensión, funciones difíciles de evaluar y funciones con singularidades o discontinuidades la convierten en una herramienta poderosa y versátil en el campo de la computación numérica.

Cuáles son los pasos para realizar una integración por Monte Carlo en Mathematica

La integración por Monte Carlo es un método numérico ampliamente utilizado para aproximar el valor de integrales que no pueden resolverse de manera analítica. En Mathematica, este proceso se simplifica gracias a las herramientas y funciones integradas en el software.

El primer paso para realizar una integración por Monte Carlo en Mathematica es definir la función que se desea integrar. Para esto, se puede utilizar la función "f:=..." seguida de la expresión matemática de la función.

A continuación, es necesario especificar el dominio de integración. Esto se puede hacer utilizando las funciones "Region" y "ImplicitRegion" de Mathematica, dependiendo de la naturaleza del dominio.

Una vez que se ha definido la función y el dominio de integración, se procede a generar los puntos aleatorios que se utilizarán en el cálculo de la integral. Esto se puede hacer utilizando la función "RandomPoint" junto con el dominio de integración especificado anteriormente.

Luego, se evalúa la función en cada uno de los puntos generados y se calcula la media de los valores obtenidos. Esto se puede hacer utilizando la función "Mean".

Finalmente, se multiplica la media de los valores obtenidos por el volumen del dominio de integración para obtener una aproximación de la integral. El volumen del dominio de integración se puede calcular utilizando la función "Volume" de Mathematica.

Los pasos para realizar una integración por Monte Carlo en Mathematica son: definir la función, especificar el dominio de integración, generar los puntos aleatorios, evaluar la función en los puntos generados, calcular la media de los valores obtenidos y multiplicar por el volumen del dominio de integración.

A continuación, se mostrará un ejemplo paso a paso de cómo realizar una integración por Monte Carlo en Mathematica utilizando una función y un dominio de integración específicos.

Qué tipos de funciones se pueden integrar utilizando este método

La integración por Monte Carlo es un método poderoso para evaluar integrales que no tienen una solución analítica. Este método se puede utilizar para integrar cualquier tipo de función, ya sea continua, discontinua, unidimensional o multidimensional. Es especialmente útil cuando se enfrenta a integrales complejas que son difíciles de resolver utilizando métodos tradicionales. No hay restricciones sobre el tipo de funciones que se pueden integrar utilizando este método, lo que lo convierte en una herramienta versátil para los científicos, ingenieros y matemáticos.

Cuáles son los parámetros que se deben ajustar para obtener una estimación precisa de la integral

La integración por Monte Carlo es un método numérico utilizado para aproximar el valor de una integral mediante el muestreo aleatorio de puntos en el dominio de integración. Para obtener una estimación precisa de la integral, es importante ajustar correctamente los parámetros del algoritmo.

Número de puntos de muestreo

El número de puntos de muestreo es uno de los parámetros clave que se deben ajustar. Aumentar el número de puntos de muestreo generalmente conduce a una estimación más precisa, pero también aumenta el tiempo de cálculo. Por lo tanto, es necesario encontrar un equilibrio entre la precisión deseada y el tiempo de ejecución aceptable.

Distribución de los puntos de muestreo

La distribución de los puntos de muestreo también es importante para obtener una buena estimación. Idealmente, los puntos deben distribuirse de manera uniforme en todo el dominio de integración. En Mathematica, se pueden utilizar distintos generadores de números aleatorios y técnicas de muestreo para lograr una distribución adecuada de los puntos.

Función a integrar

La elección de la función a integrar también puede afectar la precisión de la estimación. Algunas funciones pueden ser más difíciles de integrar que otras, ya sea debido a su forma o su comportamiento cercano a los límites del dominio de integración. En general, es recomendable utilizar funciones que sean suaves y bien comportadas en el dominio de integración.

Tamaño del dominio de integración

El tamaño del dominio de integración también puede influir en la precisión de la estimación. Si el dominio de integración es muy grande, es posible que se necesite un mayor número de puntos de muestreo para obtener una estimación precisa. Por otro lado, si el dominio de integración es muy pequeño, es posible que el algoritmo no capture todas las características importantes de la función a integrar.

Variación de los resultados

Finalmente, es importante tener en cuenta la variación de los resultados al ajustar los parámetros de la integración por Monte Carlo. En ocasiones, puede haber fluctuaciones significativas en las estimaciones, incluso con un número suficientemente grande de puntos de muestreo. En tales casos, es útil realizar múltiples ejecuciones del algoritmo y promediar los resultados para obtener una estimación más estable.

Ajustar adecuadamente estos parámetros permitirá obtener estimaciones más precisas de integrales utilizando el método de Monte Carlo en Mathematica.

Es posible evaluar una integral definida utilizando la integración por Monte Carlo en Mathematica

La integración por Monte Carlo es un método numérico utilizado para estimar el valor de una integral definida. A diferencia de los métodos tradicionales, este enfoque se basa en la generación aleatoria de puntos en el espacio de integración y el cálculo de la función en esos puntos. En Mathematica, este algoritmo se implementa a través de la función NIntegrate. A continuación, te mostraré cómo utilizar este método paso a paso en Mathematica para obtener una aproximación de una integral definida.

Paso 1: Definir la función a integrar

Antes de comenzar, debemos definir la función que deseamos integrar. Para hacerlo, utilizaremos la sintaxis de Mathematica. Por ejemplo, consideremos la siguiente función:

f := Sin

En este caso, estamos definiendo la función f como el seno de x. Puedes reemplazar esta función por cualquier otra que quieras integrar.

Paso 2: Establecer los límites de integración

Una vez que hayamos definido la función, debemos establecer los límites de integración. En este ejemplo, supongamos que deseamos integrar la función f en el intervalo . Por ejemplo, supongamos que queremos integrar en el intervalo . Podemos hacerlo de la siguiente manera:

a = 0;
b = Pi;

En este caso, hemos fijado a en 0 y b en π. Puedes modificar estos valores según tus necesidades.

Paso 3: Definir el número de puntos de muestreo

El siguiente paso es definir el número de puntos de muestreo que se utilizarán en el algoritmo de integración por Monte Carlo. Cuanto mayor sea el número de puntos, mejor será la precisión de la aproximación. Sin embargo, también aumentará el tiempo de cálculo. Por ahora, supongamos que queremos usar 1000 puntos de muestreo. Podemos definir esta cantidad de la siguiente manera:

n = 1000;

Este valor de n puede ajustarse según tus necesidades.

Paso 4: Aplicar el algoritmo de integración por Monte Carlo

Con la función definida, los límites de integración establecidos y el número de puntos de muestreo determinado, estamos listos para aplicar el algoritmo de integración por Monte Carlo en Mathematica. Para hacerlo, utilizaremos la función NIntegrate. La sintaxis general es la siguiente:

NIntegrate, {x, a, b}, Method -> "MonteCarlo", WorkingPrecision -> p, PrecisionGoal -> g, MaxPoints -> n]

En esta expresión, debemos reemplazar f por la función que estamos integrando, {x, a, b} por los límites de integración, p por la precisión de trabajo deseada, g por la precisión objetivo deseada y n por el número de puntos de muestreo.

Qué opciones adicionales ofrece Mathematica para mejorar la precisión de la estimación de la integral

En la estimación de la integral, Mathematica ofrece varias opciones adicionales para mejorar la precisión. Una de estas opciones es la posibilidad de especificar el número de puntos de muestra utilizados en el método de Monte Carlo. Cuanto mayor sea el número de puntos, mayor será la precisión de la estimación, pero también aumentará el tiempo de cálculo.

Otra opción es la variación de la semilla aleatoria utilizada en el método de Monte Carlo. Al cambiar la semilla aleatoria, podemos obtener diferentes estimaciones de la integral y calcular el error promedio. Esto nos ayudará a evaluar la convergencia del método y ajustar los parámetros de la estimación.

También podemos utilizar la opción de reducción de varianza, que utiliza técnicas como la importancia del muestreo o el muestreo estratificado para mejorar la eficiencia del método de Monte Carlo. Estas técnicas permiten reducir la varianza de la estimación de la integral, lo que se traduce en una mayor precisión.

Finalmente, Mathematica también nos permite utilizar el método de Monte Carlo en regiones de integración más complejas, como por ejemplo, regiones con restricciones o regiones definidas por ecuaciones implícitas. Para esto, podemos utilizar la opción de región de integración, donde especificamos las restricciones o ecuaciones que definen la región en la que queremos realizar la estimación de la integral.

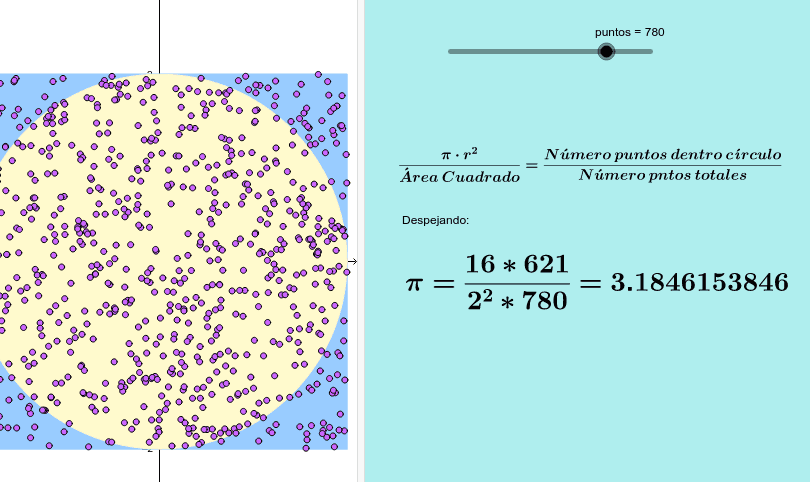
Cómo se puede visualizar el proceso de integración por Monte Carlo en Mathematica

La integración por Monte Carlo es un método numérico utilizado para aproximar integrales definidas. En Mathematica, este proceso se puede visualizar de manera sencilla mediante el uso de gráficos. En este tutorial paso a paso, te mostraré cómo implementar este método en Mathematica y cómo visualizar el proceso a través de gráficos interactivos.

Paso 1: Definir la función a integrar

El primer paso para utilizar el método de integración por Monte Carlo en Mathematica es definir la función que deseamos integrar. Por ejemplo, consideremos la función f(x) = x^2. Podemos definir esta función en Mathematica de la siguiente manera:

f := x^2

Una vez que hemos definido la función, podemos proceder al siguiente paso.

Paso 2: Generar puntos aleatorios

Para aproximar la integral, necesitamos generar puntos aleatorios dentro del rango de integración. En este caso, supongamos que queremos integrar la función f(x) en el intervalo . Podemos generar puntos aleatorios utilizando la función RandomReal de Mathematica:

points = RandomReal

Donde 'a' y 'b' son los límites del intervalo y 'n' es el número de puntos aleatorios que deseamos generar.

Paso 3: Evaluar la función en los puntos aleatorios

Una vez que hemos generado los puntos aleatorios, necesitamos evaluar la función f(x) en estos puntos. Podemos utilizar la función Map para aplicar la función a cada elemento de la lista de puntos:

evaluations = Map

Esto nos dará una lista de los valores de la función evaluados en los puntos aleatorios.

Paso 4: Calcular el promedio de los valores de la función

El siguiente paso es calcular el promedio de los valores de la función evaluados en los puntos aleatorios. Esto se puede hacer utilizando la función Mean de Mathematica:

mean = Mean

El valor de la media nos dará una aproximación de la integral de la función en el intervalo dado.

Paso 5: Visualizar el proceso de integración

Para visualizar el proceso de integración por Monte Carlo, podemos utilizar gráficos interactivos en Mathematica. Por ejemplo, podemos graficar los puntos aleatorios en el intervalo de integración y resaltar aquellos que se encuentran debajo de la curva de la función:

ListPlot, Epilog -> {Red, Point, #] <= f]] &]]}, PlotRange -> All]

Esto nos dará un gráfico interactivo donde podemos observar los puntos aleatorios y cómo se distribuyen en relación a la función que estamos integrando.

Paso 6: Calcular el área bajo la curva

Finalmente, podemos utilizar el valor promedio de los valores de la función y el tamaño del intervalo de integración para calcular el área bajo la curva. Esto se puede hacer multiplicando el promedio de los valores por la longitud del intervalo:

area = mean (b - a)

La cantidad obtenida será una aproximación del área bajo la curva de la función en el intervalo .

La integración por Monte Carlo en Mathematica es un proceso sencillo que puede ser visualizado mediante gráficos interactivos. Siguiendo los pasos descritos en esta guía, podrás utilizar este método numérico para aproximar integrales definidas de manera eficiente.

Existen alternativas a la integración por Monte Carlo en Mathematica? ¿Cuándo se recomienda utilizar cada método

Si bien la integración por Monte Carlo es una técnica poderosa y ampliamente utilizada en Mathematica, existen otras alternativas que pueden ser más adecuadas para ciertos problemas. Uno de estos métodos es la integración numérica determinística, que utiliza fórmulas matemáticas específicas para calcular el valor de la integral. Este método puede ser especialmente útil cuando la función a integrar es suave y se conoce su forma analítica.

Otra alternativa es la cuadratura numérica, que divide el dominio de integración en pequeñas regiones y luego aproxima el valor de la integral sumando los valores de la función en cada región ponderados por un conjunto de pesos específicos. Este método puede ser más eficiente que la integración por Monte Carlo en problemas en los que la función a integrar es suave y presenta una alta regularidad.

En general, se recomienda utilizar la integración por Monte Carlo cuando ninguna de estas alternativas es viable o cuando se necesita una aproximación no determinística que permita estimar el error de la integral. Además, este método puede ser especialmente útil en problemas multidimensionales, donde las alternativas pueden volverse computacionalmente costosas.

Es posible utilizar la integración por Monte Carlo en aplicaciones prácticas fuera del ámbito matemático

La integración por Monte Carlo es una técnica matemática ampliamente utilizada para estimar el valor de una integral numéricamente. Sin embargo, esta técnica no se limita solo al campo de las matemáticas, sino que también tiene aplicaciones prácticas en otros ámbitos.

Por ejemplo, en el campo de la física, la integración por Monte Carlo puede utilizarse para simular fenómenos físicos complejos. Muchas simulaciones de partículas, como las utilizadas en la física de partículas, requieren cálculos de integrales complicadas. La integración por Monte Carlo proporciona una forma eficiente de estimar estos valores y obtener resultados precisos.

Además, la integración por Monte Carlo también se utiliza en la ingeniería. Por ejemplo, en el diseño de circuitos integrados, se pueden usar técnicas de Monte Carlo para estimar la probabilidad de fallos en un circuito debido a la variabilidad de los componentes.

La integración por Monte Carlo es una herramienta poderosa que no se limita solo al ámbito matemático. Su capacidad para estimar el valor de una integral numéricamente la hace aplicable en una amplia gama de campos, desde la física hasta la ingeniería.

Preguntas frecuentes (FAQ)

¿Qué es la integración por Monte Carlo?

La integración por Monte Carlo es un método numérico utilizado para estimar el valor de una integral utilizando el muestreo aleatorio.

¿Cuándo se utiliza la integración por Monte Carlo?

La integración por Monte Carlo se utiliza cuando la función a integrar es difícil de evaluar analíticamente o cuando se tienen múltiples dimensiones.

¿Cuál es el principio detrás de la integración por Monte Carlo?

El principio detrás de la integración por Monte Carlo es utilizar números aleatorios para aproximar el valor de la integral, generando múltiples puntos dentro del dominio de integración.

¿Cómo se implementa la integración por Monte Carlo en Mathematica?

En Mathematica, se puede implementar la integración por Monte Carlo utilizando la función RandomReal para generar los puntos aleatorios y la función Mean para calcular la media de los valores de la función evaluada en los puntos generados.

¿Cuáles son las ventajas de la integración por Monte Carlo?

Algunas ventajas de la integración por Monte Carlo son su simplicidad de implementación, su capacidad para manejar integrales de alta dimensionalidad y su capacidad para proporcionar estimaciones precisas incluso cuando la función presenta singularidades o discontinuidades.