Integra la curva fácilmente en Wolfram Mathematica

Así de fácil es ingresar una función en Wolfram Mathematica y calcular la integral de una curva. Esta herramienta es extremadamente útil para estudiantes, profesionales y cualquier persona que necesite realizar cálculos matemáticos de manera rápida y precisa. ¡Inténtalo tú mismo y descubre todas las posibilidades que ofrece Wolfram Mathematica!

Cuál es la sintaxis utilizada en Wolfram Mathematica para realizar cálculos de integración de curvas

Para realizar cálculos de integración de curvas en Wolfram Mathematica, se utiliza la función "Integrate". Esta función toma dos argumentos: la función que se desea integrar y la variable de integración. La sintaxis básica es la siguiente:

Integrate

Donde "función" representa la expresión matemática que se desea integrar y "variable" es la variable de integración. Por ejemplo, si se desea calcular la integral de la función f(x) = x^2, con respecto a la variable x, la sintaxis sería:

Integrate

Es importante tener en cuenta que en Wolfram Mathematica se pueden realizar cálculos de integración numérica o simbólica, dependiendo de la naturaleza de la función. En el caso de la integración numérica, se utilizan métodos numéricos para obtener una aproximación del valor de la integral. En cambio, en la integración simbólica, Mathematica utiliza algoritmos simbólicos para obtener una expresión algebraica exacta de la integral.

Existen funciones predefinidas en Wolfram Mathematica que facilitan la integración de curvas específicas

Wolfram Mathematica es un software ampliamente utilizado en matemáticas y ciencias computacionales. Una de las ventajas de este programa es la capacidad de integrar curvas de manera sencilla y eficiente. Para aquellos que buscan una solución rápida y precisa, Mathematica ofrece una serie de funciones predefinidas que pueden ser utilizadas para integrar diferentes tipos de curvas.

Una de estas funciones es la función "Integrate", que permite calcular integrales definidas e indefinidas en varios dominios. Además, Mathematica ofrece funciones específicas para la integración de curvas cerradas, como "LineIntegral" y "PathIntegral". Estas funciones se pueden utilizar para integrar curvas en el plano complejo, así como para calcular la integral de línea a lo largo de una curva paramétrica en el espacio tridimensional.

Para utilizar estas funciones, simplemente se debe especificar la curva y los límites de integración. Mathematica realizará automáticamente los cálculos necesarios y proporcionará la solución en forma numérica o simbólica, según sea necesario. Esto hace que la integración de curvas sea más accesible y menos propensa a errores para los usuarios de Mathematica.

Además de las funciones predefinidas, Mathematica también permite a los usuarios definir sus propias funciones de integración de curvas personalizadas. Esto brinda una mayor flexibilidad y control sobre los cálculos, permitiendo adaptar la integración a necesidades específicas.

La integración de curvas en Wolfram Mathematica se simplifica enormemente gracias a las funciones predefinidas y la posibilidad de definir funciones personalizadas. Con estas herramientas, los usuarios pueden realizar cálculos numéricos y simbólicos de manera rápida y precisa, ahorrando tiempo y esfuerzo en la resolución de integrales de curvas complejas.

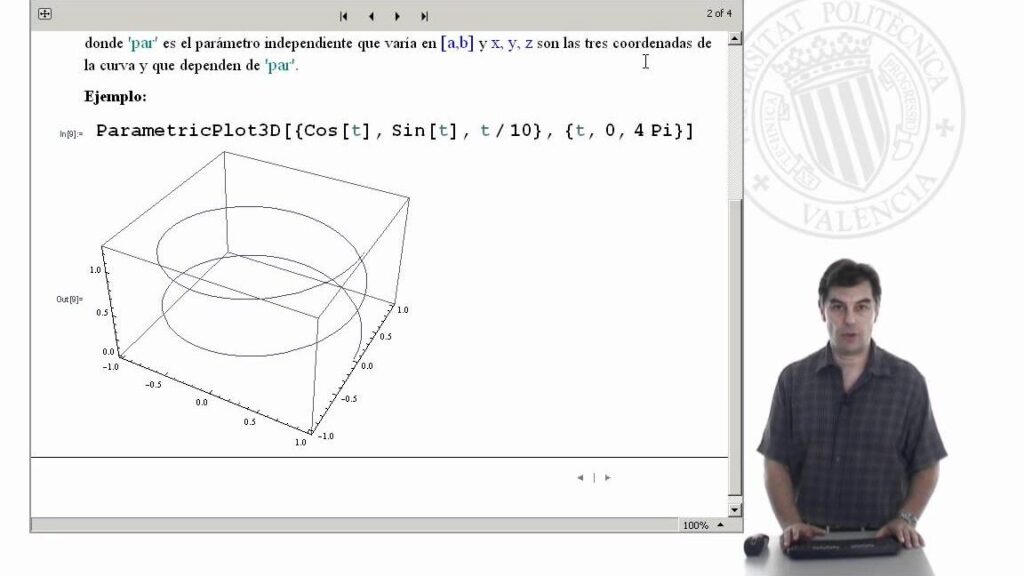
Es posible graficar una curva y calcular su integral al mismo tiempo en Wolfram Mathematica

Wolfram Mathematica es una potente herramienta de software que permite a los usuarios realizar cálculos matemáticos complejos de manera eficiente. Una de las características más destacadas de Mathematica es su capacidad para integrar funciones y graficar curvas simultáneamente.

La integración de una curva en Mathematica es sorprendentemente sencilla. Todo lo que necesitas hacer es definir la función a integrar, especificar los límites de integración y Mathematica se encargará del resto. Además, Mathematica ofrece una amplia gama de opciones para personalizar la apariencia de la curva y la visualización de los resultados.

Para comenzar, simplemente abre Mathematica y crea una nueva celda de código. Luego, define la función que deseas integrar utilizando la notación matemática estándar. Por ejemplo, si deseas integrar la función f(x) = x^2, simplemente escribe "f := x^2".

A continuación, utiliza la función "Plot" para graficar la curva de la función. Esta función acepta varios argumentos, incluyendo la función a graficar, los límites de integración y opciones de visualización adicionales. Por ejemplo, puedes utilizar la opción "PlotRange" para especificar el rango de los ejes x e y.

Una vez que hayas graficado la curva, puedes usar la función "Integrate" para calcular la integral de la función. Simplemente escribe "Integrate, {x, a, b}]", donde "f" es la función a integrar y "{x, a, b}" son los límites de integración.

Por supuesto, Mathematica también te permite realizar cálculos más avanzados, como encontrar la integral definida de una función en términos de una variable simbólica. Esto es extremadamente útil para resolver problemas matemáticos más complejos que involucran integrales.

Wolfram Mathematica facilita la integración de curvas al combinar la capacidad de graficar y calcular integrales en una sola herramienta. Si necesitas realizar cálculos matemáticos que involucren integrales, Mathematica es una excelente opción que te ahorrará tiempo y esfuerzo.

Cuál es la precisión de los resultados obtenidos al utilizar Wolfram Mathematica para la integración de curvas

Al utilizar Wolfram Mathematica para la integración de curvas, es importante tener en cuenta la precisión de los resultados obtenidos. A diferencia de otros métodos numéricos, Mathematica utiliza algoritmos avanzados que garantizan resultados muy precisos. Sin embargo, es necesario considerar que la precisión puede variar dependiendo de la función a integrar y los parámetros utilizados en la configuración del método de integración.

Es recomendable utilizar la función integrar de Mathematica junto con los parámetros adecuados para obtener resultados más precisos. Por ejemplo, si se requiere una mayor precisión, se puede especificar el valor de la opción PrecisionGoal o utilizar el método de integración adaptativa de Mathematica, que ajusta automáticamente la precisión según la función a integrar.

Es importante mencionar que, aunque Wolfram Mathematica ofrece una gran precisión en la integración de curvas, siempre es recomendable verificar los resultados obtenidos utilizando métodos analíticos o comparándolos con resultados conocidos. De esta manera, se puede asegurar la confiabilidad de los resultados y evitar posibles errores o imprecisiones en el cálculo de las integrales.

Wolfram Mathematica proporciona una precisión muy alta en la integración de curvas, pero es necesario tener en cuenta la configuración de los parámetros y verificar los resultados obtenidos. Utilizar la función integrar de Mathematica junto con los parámetros adecuados y comparar los resultados con métodos analíticos son buenas prácticas para garantizar la precisión de los cálculos.

Qué otros métodos de integración de curvas se pueden utilizar en Wolfram Mathematica además de la integración numérica

Además de la integración numérica, Wolfram Mathematica ofrece una amplia gama de métodos para integrar curvas. Uno de ellos es la integración simbólica, que utiliza técnicas de álgebra computacional para encontrar una expresión analítica exacta para la integral de una curva. Esto es especialmente útil cuando se busca una solución precisa y general.

Otro método interesante es la integración aproximada, que utiliza técnicas de interpolación para estimar el área bajo la curva. Este enfoque es especialmente útil cuando la función que se desea integrar no tiene una expresión analítica simple.

Además, Wolfram Mathematica también ofrece métodos numéricos avanzados, como la integración numérica adaptativa y la integración por cuadratura. Estos métodos permiten obtener resultados precisos y eficientes, incluso para curvas complejas o funciones con comportamiento irregular.

Wolfram Mathematica ofrece una amplia variedad de métodos de integración de curvas, lo que permite a los usuarios elegir el enfoque que mejor se adapte a sus necesidades específicas. Ya sea que se trate de integración simbólica, aproximada o numérica, Mathematica ofrece las herramientas necesarias para abordar cualquier problema de integración de curvas.

Cuál es la diferencia entre la integración de una curva cerrada y una curva abierta en Wolfram Mathematica

Al trabajar con Wolfram Mathematica, es importante comprender la diferencia entre la integración de una curva cerrada y una curva abierta. La integración de una curva cerrada implica que el camino de la curva forma un bucle cerrado, mientras que la integración de una curva abierta implica que el camino de la curva no se cierra.

Para realizar la integración de una curva cerrada en Wolfram Mathematica, se utiliza la función Integrate junto con la especificación del camino de la curva cerrada. Esto permite calcular el valor de la integral a lo largo de toda la curva cerrada.

Por otro lado, si se desea realizar la integración de una curva abierta en Wolfram Mathematica, se debe utilizar la función NIntegrate. Esta función permite obtener una aproximación numérica del valor de la integral a lo largo del camino de la curva abierta.

Wolfram Mathematica cuenta con herramientas para realizar tanto la integración de una curva cerrada como de una curva abierta. La elección de la función a utilizar dependerá del tipo de curva y del objetivo de la integración.

Puedo utilizar Wolfram Mathematica para encontrar la longitud de una curva utilizando la integral

Wolfram Mathematica es una poderosa herramienta matemática que permite realizar cálculos complejos de manera eficiente. Una de las funcionalidades más interesantes que ofrece es la capacidad de encontrar la longitud de una curva utilizando la integral. Esta herramienta es especialmente útil en campos como la física y la geometría, donde se requiere determinar la longitud de una curva en un espacio tridimensional. La integración en Mathematica es rápida y precisa, lo que permite obtener resultados confiables en poco tiempo.

Para utilizar esta funcionalidad, simplemente necesitas tener instalado Mathematica en tu computadora o acceder a su versión en línea. Una vez que hayas abierto el programa, podrás ingresar la función de la curva en la que estás interesado y especificar los límites de integración. Mathematica generará automáticamente la integral correspondiente y calculará su resultado en cuestión de segundos.

Paso 1: Definir la función de la curva

El primer paso para encontrar la longitud de una curva en Mathematica es definir la función que representa dicha curva. Esto implica establecer la relación entre las variables x e y que describen la curva. Por ejemplo, si estás trabajando con una curva en el plano cartesiano, podrías tener una función de la forma y = f(x).

Es importante tener en cuenta que la función debe ser continua y diferenciable en el intervalo de interés. Si la función no cumple con estas condiciones, es posible que Mathematica no pueda encontrar la longitud de la curva utilizando la integral. En caso de que la función sea discontinua o no diferenciable, es posible utilizar aproximaciones numéricas para obtener una estimación de la longitud.

Paso 2: Especificar los límites de integración

Una vez que hayas definido la función de la curva, es necesario especificar los límites de integración. Estos límites determinan el intervalo en el que se calculará la longitud de la curva. Por ejemplo, si estás interesado en encontrar la longitud de la curva en el intervalo , deberás ingresar estos valores como límites de integración en Mathematica.

Es importante asegurarse de que los límites de integración estén dentro del dominio de la función. Si intentas calcular la longitud de una curva más allá de los límites de la función, es posible que obtengas un resultado incorrecto o un mensaje de error por parte de Mathematica.

Paso 3: Calcular la integral y obtener la longitud de la curva

Una vez que hayas definido la función de la curva y especificado los límites de integración, puedes utilizar Mathematica para calcular la integral y obtener la longitud de la curva. Esto se logra utilizando la función "Integrate" seguida de la función que representa la curva y los límites de integración.

Mathematica evaluará la integral y te proporcionará el resultado, que corresponderá a la longitud de la curva. Este resultado puede ser un número exacto o una expresión simbólica, dependiendo de la complejidad de la función y los límites de integración.

Es importante destacar que Mathematica también ofrece la posibilidad de calcular integrales definidas numéricamente en caso de que no sea posible obtener una solución exacta. Esto puede ser útil en situaciones en las que la función de la curva o los límites de integración sean demasiado complejos para ser resueltos de manera analítica.

Utilizar Wolfram Mathematica para encontrar la longitud de una curva utilizando la integral es una forma eficiente y precisa de realizar este cálculo. Siguiendo los pasos mencionados anteriormente, podrás obtener resultados confiables en poco tiempo. Esta funcionalidad es especialmente útil en campos como la física y la geometría, donde la longitud de una curva es una medida fundamental para comprender fenómenos y propiedades de los objetos en el espacio tridimensional.

En qué casos puedo utilizar la integración de curvas en Wolfram Mathematica en mi trabajo o investigación

La integración de curvas en Wolfram Mathematica es una herramienta poderosa que puede ser utilizada en una variedad de casos en tu trabajo o investigación. Si estás trabajando en física, puedes utilizar esta función para calcular el trabajo realizado por una fuerza a lo largo de una trayectoria curva. También puede ser útil en matemáticas, por ejemplo, al calcular la longitud de una curva o al encontrar el área entre una curva y el eje x. En ciencias de la computación, la integración de curvas puede ser utilizada en algoritmos de procesamiento de imágenes para reconstruir formas complejas. Sea cual sea tu campo, la integración de curvas en Wolfram Mathematica puede ayudarte a resolver problemas de manera r rápida y precisa.

Preguntas frecuentes (FAQ)

¿Qué es la curva en Wolfram Mathematica?

La curva en Wolfram Mathematica es una función que representa una línea en un plano.

¿Cómo puedo integrar una curva en Wolfram Mathematica?

Puedes integrar una curva en Wolfram Mathematica utilizando la función "Integrate" y especificando la función de la curva.

¿Qué es la integral de una curva?

La integral de una curva es el área bajo la curva, que se calcula sumando todos los valores de la función en un rango determinado.

¿Qué información necesito para integrar una curva en Wolfram Mathematica?

Para integrar una curva en Wolfram Mathematica, necesitas conocer la función de la curva y el rango sobre el cual quieres calcular el área.

¿Puedo integrar una curva en Wolfram Mathematica si no conozco la función exacta?

No, para integrar una curva en Wolfram Mathematica, necesitas conocer la función exacta de la curva. Si no conoces la función, no podrás realizar la integración.