Función logaritmo natural en Mathematica: guía y ejemplos

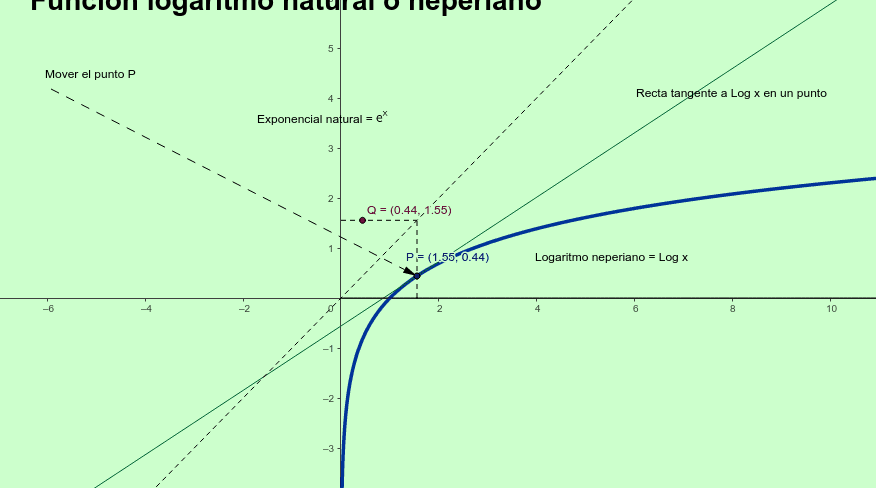
El logaritmo natural es una función matemática muy utilizada en diversos campos, desde el cálculo hasta la estadística y la física. Su importancia radica en su capacidad para describir el comportamiento de fenómenos que crecen o disminuyen de forma exponencial. En el ámbito de la programación, especialmente en el lenguaje de programación Mathematica, el logaritmo natural también es una herramienta fundamental.

Exploraremos detalladamente la función logaritmo natural en Mathematica. Veremos cómo utilizarla eficientemente, así como sus diferentes aplicaciones prácticas. También incluiremos ejemplos y ejercicios que te permitirán familiarizarte con su uso y profundizar en tu comprensión de esta poderosa función.

Cómo se utiliza la función logaritmo natural en Mathematica

En Mathematica, la función logaritmo natural se representa mediante Log. Esta función calcula el logaritmo natural de un número, es decir, el logaritmo en base e.

Para utilizar la función logaritmo natural en Mathematica, simplemente se debe ingresar el número dentro de los corchetes, por ejemplo: Log calculará el logaritmo natural de 10.

Es importante tener en cuenta que el argumento de la función logaritmo natural debe ser un número real y mayor que cero. De lo contrario, Mathematica devuelve un mensaje de error.

La función logaritmo natural también se puede utilizar para calcular logaritmos naturales de expresiones más complejas. Por ejemplo, Log calculará el logaritmo natural del cuadrado de x.

Cuál es la sintaxis correcta para calcular el logaritmo natural de un número en Mathematica

En Mathematica, puedes calcular el logaritmo natural de un número utilizando la función Log. La sintaxis correcta es Log, donde x representa el número del cual deseas calcular el logaritmo natural. Por ejemplo, si deseas calcular el logaritmo natural de 2, puedes escribir Log.

Es importante tener en cuenta que el número x debe ser positivo para que el cálculo sea válido. Si intentas calcular el logaritmo natural de un número negativo o cero, Mathematica mostrará un mensaje de error.

Además, es posible especificar una base diferente para el logaritmo utilizando la sintaxis Log, donde b representa la base del logaritmo y x el número. Por ejemplo, si deseas calcular el logaritmo en base 10 de 100, puedes escribir Log.

Qué ventajas tiene utilizar Mathematica para calcular logaritmos naturales en comparación con otras herramientas

Mathematica es una poderosa herramienta para realizar cálculos matemáticos y científicos, y calcular logaritmos naturales no es una excepción. Una de las principales ventajas de utilizar Mathematica para este propósito es su capacidad para manejar números de precisión arbitraria, lo que garantiza resultados precisos incluso para valores muy grandes o muy pequeños. Además, Mathematica proporciona una amplia gama de funciones y características para trabajar con logaritmos naturales, como la posibilidad de obtener gráficos de funciones logarítmicas y realizar operaciones matemáticas complejas utilizando estos logaritmos.

Otra ventaja importante de utilizar Mathematica para calcular logaritmos naturales es su facilidad de uso. La sintaxis clara y concisa de Mathematica hace que sea sencillo escribir y evaluar expresiones logarítmicas, lo que ahorra tiempo y esfuerzo al usuario. Además, Mathematica proporciona una amplia documentación y ejemplos de uso de la función logaritmo natural, lo que facilita el aprendizaje y la comprensión de su uso. Utilizar Mathematica para calcular logaritmos naturales es una opción inteligente debido a su precisión, versatilidad y facilidad de uso.

Existen funciones relacionadas con el logaritmo natural en Mathematica que puedan ser útiles en cálculos más avanzados

En el software Mathematica, existen varias funciones relacionadas con el logaritmo natural que pueden ser útiles en cálculos más avanzados. Una de ellas es la función Log, que calcula el logaritmo natural de un número dado. Esta función es especialmente útil cuando se trabaja con problemas relacionados con crecimiento exponencial o tasas de cambio.

Ejemplo de uso de la función Log en Mathematica

Supongamos que queremos calcular el tiempo que tarda una población en duplicarse, dada una tasa de crecimiento constante. Podemos utilizar la función Log para resolver este problema de manera sencilla en Mathematica.

Por ejemplo, si tenemos una población inicial de 1000 individuos y la tasa de crecimiento es del 5% anual, podemos utilizar la siguiente fórmula para calcular el tiempo necesario para que la población se duplique:

tiempo = Log/Log

La expresión Log representa el logaritmo natural de 2, que es aproximadamente 0.6931, y Log representa el logaritmo natural de 1.05, que es aproximadamente 0.0488. Al dividir Log por Log, obtendremos el tiempo necesario para que la población se duplique, que en este caso es aproximadamente 14.206 años.

Otras funciones relacionadas con el logaritmo natural en Mathematica

Además de la función Log, Mathematica ofrece otras funciones relacionadas con el logaritmo natural que pueden resultar útiles en diferentes contextos. Algunas de estas funciones incluyen:

• Log10: calcula el logaritmo en base 10 de un número dado.
• Log2: calcula el logaritmo en base 2 de un número dado.
• Exp: calcula el exponencial de un número dado.

Estas funciones pueden resultar especialmente útiles cuando se trabaja con problemas que involucran diferentes bases logarítmicas o cuando se necesita calcular el exponencial de un número. Mathematica ofrece una serie de funciones relacionadas con el logaritmo natural que pueden facilitar el trabajo con cálculos más avanzados.

Es posible calcular logaritmos naturales de números complejos en Mathematica

En Mathematica, podemos usar la función Log para calcular el logaritmo natural de un número complejo. Esta función acepta números reales y complejos como argumentos y devuelve el logaritmo natural correspondiente. Por ejemplo, para calcular el logaritmo natural de un número complejo, simplemente escribimos Log.

Además de calcular el logaritmo natural de un número complejo, Mathematica también nos permite calcular el logaritmo natural de una lista de números complejos. Podemos utilizar la función Map junto con Log para aplicar la función a cada elemento de la lista. Por ejemplo, si tenemos una lista lista de números complejos, podemos escribir Map para obtener la lista de logaritmos naturales correspondientes.

Es importante tener en cuenta que el logaritmo natural de un número complejo puede ser un número complejo también. Por lo tanto, la función Log en Mathematica devuelve un número complejo cuando se le pasa un número complejo como argumento. Si deseamos obtener la parte real o imaginaria del logaritmo natural de un número complejo, podemos utilizar las funciones Re e Im respectivamente. Por ejemplo, Re] nos dará la parte real del logaritmo natural de z.

Cuál es la precisión de los cálculos de logaritmo natural en Mathematica

La precisión de los cálculos de logaritmo natural en Mathematica es uno de los aspectos más importantes a tener en cuenta al trabajar con esta función. Por defecto, Mathematica utiliza una precisión de 16 dígitos decimales, lo cual es suficiente para la mayoría de los casos. Sin embargo, si requieres una mayor precisión, puedes ajustarla utilizando la opción "WorkingPrecision" al llamar a la función Log en Mathematica.

Por ejemplo, si deseas calcular el logaritmo natural de un número con una precisión de 30 dígitos decimales, puedes utilizar la siguiente sintaxis:

Log

Esto asegurará que los cálculos se realicen con la precisión deseada. Sin embargo, cabe destacar que trabajar con una mayor precisión puede resultar en un mayor consumo de recursos computacionales y un mayor tiempo de ejecución.

Es posible graficar la función logaritmo natural en Mathematica

En Mathematica, podemos utilizar la función "Log" para calcular el logaritmo natural de un número. Para graficar la función logaritmo natural, podemos usar la función "Plot". Por ejemplo, para graficar el logaritmo natural en el intervalo de -10 a 10, podemos escribir:

Plot, {x, -10, 10}]

Esto generará una gráfica de la función logaritmo natural en el intervalo dado. También podemos personalizar la apariencia de la gráfica agregando etiquetas a los ejes, títulos y leyendas.

Además, podemos utilizar la función "LogPlot" en lugar de "Plot" para generar una gráfica donde el eje y está en escala logarítmica, lo cual puede ser útil en ciertos casos.

Existe alguna función en Mathematica para calcular logaritmos naturales en base 10

Sí, en Mathematica existe una función específica para calcular logaritmos naturales en base 10. Esta función se llama "Log10" y se utiliza de la siguiente manera:

```mathematica
Log10
```

Donde "x" representa el número al cual se le quiere calcular su logaritmo en base 10. Por ejemplo, si quisieras calcular el logaritmo en base 10 de 100, simplemente ingresarías:

```mathematica
Log10
```

El resultado que obtendrías sería:

```mathematica
2
```

Es importante destacar que la función "Log10" solo acepta números reales positivos como argumento.

Cómo se puede utilizar el logaritmo natural en ecuaciones y sistemas de ecuaciones en Mathematica

El logaritmo natural, también conocido como logaritmo neperiano, es una función matemática muy utilizada en diferentes áreas de la ciencia y la ingeniería. En el ámbito de la programación y el análisis numérico, el lenguaje de programación Mathematica ofrece diferentes formas de utilizar esta función en ecuaciones y sistemas de ecuaciones.

En Mathematica, para calcular el logaritmo natural de un número o una expresión, se utiliza la función Log, donde x representa el número o la expresión de la cual se desea calcular el logaritmo natural.

Por ejemplo, si queremos calcular el logaritmo natural de 10, simplemente escribimos Log y Mathematica nos devolverá el resultado: 2.30259.

Además de calcular el logaritmo natural de un solo número, también es posible utilizar esta función en ecuaciones y sistemas de ecuaciones. Por ejemplo, supongamos que tenemos la siguiente ecuación:

x^2 - 5x + Log - 1 == 0

Podemos utilizar la función FindRoot de Mathematica para encontrar las soluciones de esta ecuación. La sintaxis sería la siguiente:

FindRoot - 1 == 0, {x, 1}]

En este caso, estamos indicando que queremos encontrar la raíz de la ecuación x^2 - 5x + Log - 1 == 0 partiendo de una estimación inicial de x = 1. Mathematica nos dará como resultado el valor de x que satisface la ecuación.

Además de ecuaciones simples, también es posible utilizar el logaritmo natural en sistemas de ecuaciones. Por ejemplo, supongamos que tenemos el siguiente sistema de ecuaciones:

{x^2 - y == 10, x/y + Log == 5}

Para resolver este sistema de ecuaciones, podemos utilizar la función Solve de Mathematica. La sintaxis sería la siguiente:

Solve == 5}, {x, y}]

En este caso, estamos indicando que queremos encontrar los valores de x e y que satisfacen el sistema de ecuaciones. Mathematica nos dará como resultado una lista de reglas que representan las soluciones del sistema.

El logaritmo natural es una función muy útil en el análisis numérico y Mathematica ofrece diferentes formas de utilizar esta función en ecuaciones y sistemas de ecuaciones. Ya sea calculando el logaritmo de un número o utilizando esta función en ecuaciones más complejas, Mathematica nos proporciona las herramientas necesarias para realizar estos cálculos de manera eficiente y precisa.

Cuáles son algunos ejemplos prácticos de cómo utilizar el logaritmo natural en Mathematica

El logaritmo natural es una función importante en Mathematica que se utiliza para calcular el logaritmo de base e de un número dado. Tiene una amplia variedad de aplicaciones en matemáticas, física, estadísticas y más.

Una de las aplicaciones más comunes del logaritmo natural es en la resolución de ecuaciones exponenciales. Por ejemplo, si tenemos la ecuación (e^x = 5), podemos utilizar la función Log para encontrar el valor de x. En Mathematica, podemos escribir:

x = Log

Esto nos dará el valor de x, que en este caso es aproximadamente 1.60944. Podemos verificarlo sustituyendo este valor de x en la ecuación original y verificando que se cumple (e^{1.60944} approx 5).

Otra aplicación práctica del logaritmo natural es en el cálculo de la tasa de crecimiento continua. Por ejemplo, si tenemos una función de la forma (f(t) = a cdot e^{kt}), donde a es una constante y k es la tasa de crecimiento, podemos utilizar el logaritmo natural para calcular el valor de k. En Mathematica, podemos hacerlo de la siguiente manera:

k = Log

Esto nos dará el valor de k, que representa la tasa de crecimiento continua de la función. Podemos utilizar este valor para realizar predicciones sobre el crecimiento futuro de la función.

El logaritmo natural es una función poderosa en Mathematica que tiene numerosas aplicaciones prácticas en diversas áreas. Ya sea para resolver ecuaciones exponenciales o calcular tasas de crecimiento continua, el logaritmo natural es una herramienta útil que todo usuario de Mathematica debe conocer y utilizar.

Es posible calcular logaritmos naturales de matrices en Mathematica

Una de las poderosas funciones que Mathematica ofrece es la capacidad de calcular logaritmos naturales de matrices. Esto resulta especialmente útil cuando se trabaja con conjuntos de datos de gran tamaño y se necesita realizar cálculos complejos. El logaritmo natural, también conocido como logaritmo en base e, es una función matemática fundamental que aparece en numerosos campos, como la ciencia, la ingeniería y la física. En este artículo, exploraremos cómo utilizar la función logaritmo natural en Mathematica, así como algunos ejemplos de su aplicación práctica.

A = {{1, 2, 3},
     {4, 5, 6},
     {7, 8, 9}}

Log

{{0, 0.693147, 1.09861},
 {1.38629, 1.60944, 1.79176},
 {1.94591, 2.07944, 2.19722}}

B = {{2, 4, 6},
     {8, 10, 12},
     {14, 16, 18}}

Log

{{0.693147, 1.38629, 1.79176},
 {2.07944, 2.30259, 2.48491},
 {2.63906, 2.77259, 2.89037}}