Cómo hallar un punto de un plano en Mathematica: trucos y consejos

Mathematica es una poderosa herramienta de software utilizada en el campo de las matemáticas y la programación. Es especialmente útil para realizar cálculos y resolver problemas complejos relacionados con el álgebra, la geometría y el cálculo. Una de las funcionalidades más interesantes de Mathematica es su capacidad para trabajar con geometría tridimensional, lo que permite realizar operaciones y cálculos relacionados con planos, puntos y vectores en el espacio.

Veremos cómo utilizar Mathematica para encontrar un punto específico en un plano tridimensional. Explicaremos los pasos necesarios para definir el plano, establecer las coordenadas del punto y realizar los cálculos necesarios para encontrar las coordenadas del punto de interés. Además, compartiremos algunos trucos y consejos útiles para aprovechar al máximo las capacidades geométricas de Mathematica.

Cuál es la sintaxis básica para definir un plano en Mathematica

En Mathematica, para definir un plano se utiliza la siguiente sintaxis:

plano = InfinitePlane;

Donde "punto" es un punto que pertenece al plano y "vectorNormal" es un vector perpendicular al plano.

Por ejemplo, si queremos definir un plano que pase por el punto (1,2,3) y tenga un vector normal de (2,1,3), la sintaxis sería:

plano = InfinitePlane;

Con esto, hemos definido el plano en Mathematica.

Cómo puedo determinar si un punto dado está en un plano o no utilizando la función "RegionMember"

La función "RegionMember" en Mathematica es una herramienta muy útil para determinar si un punto dado está contenido en un plano o no. Para utilizar esta función, primero debemos definir el plano como una región en Mathematica. Esto se puede hacer utilizando la función "InfinitePlane" y proporcionando tres puntos que estén en el plano.

Una vez que hemos definido el plano, podemos utilizar la función "RegionMember" para comprobar si un punto específico está en el plano. Por ejemplo, si tenemos el plano definido como "plano = InfinitePlane", podemos comprobar si el punto (2, 3, 4) está en el plano mediante la expresión "RegionMember". Si la expresión devuelve "True", entonces el punto está en el plano, de lo contrario, si devuelve "False", el punto no está en el plano.

Además de utilizar la función "RegionMember", también podemos utilizar otras funciones en Mathematica para determinar si un punto está en un plano. Por ejemplo, la función "RegionIntersection" nos permite calcular la intersección entre un plano y un punto específico. Si la intersección es un punto, entonces ese punto está en el plano. Si la intersección es vacía, entonces el punto no está en el plano.

Para determinar si un punto está en un plano en Mathematica, podemos utilizar la función "RegionMember" junto con la definición del plano como una región en Mathematica. También podemos utilizar otras funciones, como "RegionIntersection", para verificar la intersección entre un plano y un punto dado. Estas herramientas son muy útiles para realizar cálculos y análisis geométricos en Mathematica.

Qué métodos puedo utilizar para encontrar un punto de intersección entre un plano y una recta en Mathematica

En Mathematica, hay varios métodos que puedes utilizar para encontrar un punto de intersección entre un plano y una recta. Uno de los métodos más comunes es usando la función Solve. Puedes definir la recta y el plano como ecuaciones y luego utilizar Solve para encontrar el punto de intersección. Otra opción es utilizar la función RegionIntersection, que te permite encontrar el punto de intersección entre dos regiones en general. También puedes utilizar la función NSolve si deseas encontrar una solución numérica en lugar de una solución exacta.

Además, si estás trabajando con coordenadas tridimensionales, puedes utilizar la función Graphics3D para visualizar el plano y la recta, lo que te puede ayudar a comprender mejor las intersecciones. También puedes utilizar la función Manipulate para interactuar con la visualización y cambiar los parámetros de las ecuaciones del plano y la recta en tiempo real.

En Mathematica tienes diversas herramientas y funciones que puedes utilizar para encontrar un punto de intersección entre un plano y una recta. Puedes utilizar funciones como Solve, RegionIntersection y NSolve, y aprovechar las capacidades de visualización de Mathematica con Graphics3D y Manipulate para ayudarte en el proceso.

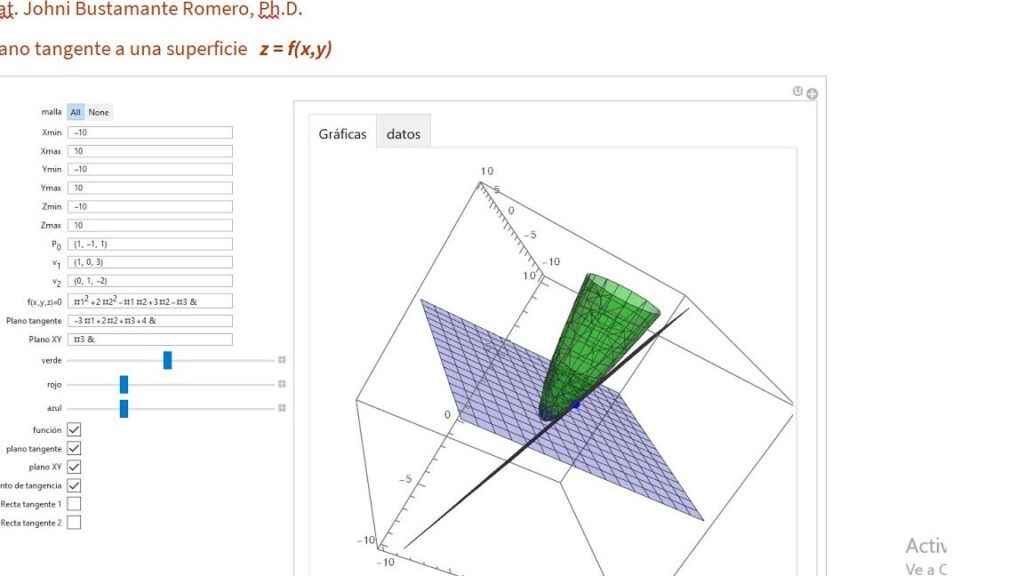
Es posible graficar un plano y un punto específico en Mathematica? De ser así, ¿cómo se hace

Sí, es posible graficar un plano y un punto específico en Mathematica. Para hacerlo, primero debemos definir el plano utilizando la función "ParametricPlot3D". Luego, podemos utilizar la función "Graphics3D" para graficar el punto en el plano. Por ejemplo, si queremos graficar el plano z = x + y y el punto (1, 2, 3), podemos hacerlo de la siguiente manera:


plano = ParametricPlot3D;
punto = Graphics3D, Point}];
Show


Este código generará una gráfica 3D del plano y el punto especificado. Puedes ajustar los límites de los ejes x, y y z según tus necesidades. Además, puedes personalizar la apariencia de la gráfica utilizando diversas opciones de estilo en las funciones "ParametricPlot3D" y "Graphics3D".

Trucos y consejos adicionales

• Si quieres visualizar mejor el plano, puedes ajustar los parámetros de los límites en la función "ParametricPlot3D". Esto te permitirá obtener una vista más cercana o más alejada del plano.
• Si deseas graficar varios puntos en el plano, puedes utilizar la función "Graphics3D" para definir una lista de puntos y luego utilizar "Show" para combinar todos los elementos gráficos en una sola imagen.
• Si deseas cambiar el tamaño o el color del punto, puedes ajustar los parámetros de "PointSize" y "Point" en la función "Graphics3D".

Mathematica ofrece herramientas poderosas para graficar planos y puntos en un entorno 3D. Con las funciones adecuadas y algunos trucos, puedes crear visualizaciones impresionantes y explorar diferentes escenarios en tus proyectos matemáticos.

Cómo puedo encontrar la ecuación de un plano dados tres puntos en Mathematica

Para encontrar la ecuación de un plano dados tres puntos en Mathematica, podemos utilizar la función "Fit" junto con la función "PlaneThrough". Primero, debemos definir los puntos utilizando la notación de coordenadas cartesianas. Después, utilizamos la función "Fit" para ajustar los puntos a una función lineal. Finalmente, utilizamos la función "PlaneThrough" para obtener la ecuación del plano que pasa por los tres puntos dados. Aquí tienes un ejemplo de cómo hacerlo:


puntos = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
ajuste = Fit;
plano = PlaneThrough;


En este ejemplo, hemos definido los puntos como una lista de listas, donde cada sublista representa las coordenadas x, y, y z de cada punto. Luego, utilizamos la función "Fit" para ajustar los puntos a una función lineal, especificando las variables x y y. Por último, utilizamos la función "PlaneThrough" para obtener la ecuación del plano que pasa por los tres puntos dados.

Es importante tener en cuenta que los puntos deben estar en un formato adecuado para que estas funciones funcionen correctamente. Además, Mathematica utiliza la convención z = ax + by + c para la ecuación del plano, donde a, b y c son los coeficientes que se encuentran en la lista de salida de la función "PlaneThrough".

Existe alguna función en Mathematica que permita calcular la distancia entre un punto y un plano

En Mathematica, podemos utilizar la función RegionDistance para calcular la distancia entre un punto y un plano.
Esta función toma como argumentos el punto y el plano en forma de región y devuelve la distancia mínima entre ellos.
Si queremos encontrar la distancia entre un punto p y un plano plano, podemos usar la siguiente sintaxis:

distancia = RegionDistance

Esta función es útil cuando necesitamos calcular la distancia entre un punto y un plano en problemas de geometría analítica.
Además, podemos utilizarla en combinación con otras funciones de Mathematica para realizar cálculos más complejos.

Cuáles son las opciones disponibles en Mathematica para visualizar un plano en un gráfico 3D

Existen varias opciones en Mathematica para visualizar un plano en un gráfico 3D. Una de ellas es utilizando la función Plot3D, que permite graficar funciones tridimensionales. Otra opción es utilizar la función Graphics3D, que permite crear objetos gráficos en tres dimensiones.

Para graficar un plano en Mathematica, se puede utilizar la función ContourPlot3D, que permite visualizar curvas de nivel en un espacio tridimensional. También se puede utilizar la función ParametricPlot3D, que permite graficar superficies mediante una parametrización.

Además, Mathematica cuenta con varias opciones de personalización para la visualización de planos en un gráfico 3D. Se pueden ajustar colores, estilos de línea y opacidades, entre otros parámetros, para obtener el resultado deseado.

Es posible encontrar la ecuación de un plano a partir de un vector normal y un punto en Mathematica? Si es así, ¿cómo se realiza

¡En Mathematica, puedes encontrar la ecuación de un plano utilizando un vector normal y un punto! Este proceso se realiza mediante la función Plane. Primero, debes definir el vector normal y el punto que deseas utilizar. Luego, simplemente llama a la función Plane con estos parámetros. Mathematica devolverá la ecuación del plano en forma de un objeto matemático. También puedes visualizar el plano utilizando la función Graphics3D. ¡Así de fácil es encontrar un punto de un plano en Mathematica!

Pero, ¿qué hacer si solo tienes la ecuación de un plano y quieres encontrar un punto en él? Auch, parece más complicado, pero no te preocupes. Afortunadamente, también existe una función en Mathematica para esto. ¡Se llama Solve! Simplemente proporciona la ecuación del plano y resuelve para las variables desconocidas. Mathematica devolverá las soluciones en forma de una lista de reglas. Estas reglas representan los puntos que se encuentran en el plano. ¡Entonces, ya sabes cómo encontrar un punto en un plano en Mathematica utilizando tanto una ecuación como un vector normal y un punto!

Ejemplo de cómo encontrar un punto de un plano en Mathematica:

normal = {2, 3, 1};
punto = {1, -2, 4};
plano = Plane;
puntos_plano = Solve;

En este ejemplo, creamos un vector normal y un punto. Luego, usamos la función Plane para obtener la ecuación del plano. Finalmente, utilizamos la función Solve para encontrar los puntos en el plano. En el resultado, tendríamos una lista de reglas que nos proporciona los puntos en el plano.

¡Recuerda que Mathematica es una herramienta poderosa para realizar cálculos matemáticos! Ya sea que necesites encontrar un punto en un plano a partir de una ecuación, un vector normal y un punto, o viceversa, Mathematica tiene las funciones necesarias para ayudarte a lograrlo. ¡Explora y aprovecha al máximo las capacidades de Mathematica!

Cuáles son las ventajas de utilizar Mathematica para resolver problemas relacionados con planos en comparación con otros software matemáticos

Mathematica es una herramienta poderosa que ofrece muchas ventajas a la hora de resolver problemas relacionados con planos. Una de las principales ventajas es su capacidad para trabajar con expresiones simbólicas y números reales, lo que permite obtener resultados exactos y aproximados. Además, Mathematica cuenta con una amplia gama de funciones y comandos específicos para manipular y visualizar planos de manera eficiente. También ofrece la posibilidad de realizar cálculos numéricos y simbólicos, lo que facilita la resolución de problemas más complejos. Mathematica es una herramienta versátil y potente para trabajar con planos.

Funciones y comandos útiles para hallar un punto de un plano en Mathematica

• RegionMember: Este comando permite verificar si un punto pertenece a un plano dado. Puede ser útil para comprobar la validez de un punto obtenido.
• Reduce: Con este comando se pueden resolver sistemas de ecuaciones en general, incluyendo ecuaciones lineales que representan un plano.
• Solve: Esta función es útil para encontrar la solución general de una ecuación lineal en forma vectorial.
• Graphics3D: Permite visualizar gráficamente un plano en un espacio tridimensional.
• ParametricPlot3D: Esta función permite graficar la intersección de un plano con otros objetos geométricos.

Trucos y consejos para resolver problemas relacionados con planos en Mathematica

1. Utilizar la función RegionMember junto con la función Graphics3D para visualizar el plano y comprobar la validez de los puntos obtenidos.
2. Si se tiene un sistema de ecuaciones lineales que representa el plano, utilizar la función Reduce para encontrar una solución particular o general.
3. En caso de que la ecuación lineal sea en forma vectorial, se puede utilizar la función Solve para encontrar una solución general.
4. Al graficar la intersección de un plano con otros objetos geométricos, utilizar la función ParametricPlot3D y experimentar con diferentes opciones de visualización.

Mathematica ofrece numerosas ventajas a la hora de resolver problemas relacionados con planos, gracias a su capacidad para trabajar con expresiones simbólicas y numéricas, así como a sus funciones y comandos específicos. Utilizando las funciones y comandos mencionados, junto con algunos trucos y consejos, es posible hallar un punto de un plano de forma eficiente y precisa.

Existen librerías adicionales en Mathematica que se puedan utilizar para trabajar con planos y puntos de forma más eficiente

Además de las funciones básicas de Mathematica, existen librerías adicionales que pueden ser utilizadas para trabajar con planos y puntos de una manera más eficiente. Estas librerías proporcionan una amplia gama de herramientas y funciones que facilitan las operaciones matemáticas relacionadas con los planos y puntos en el espacio tridimensional.

Una de las librerías más utilizadas es la librería `Graphics3D`, que ofrece una extensa colección de funciones y métodos para crear y manipular gráficos en tres dimensiones. Esta librería proporciona funciones para dibujar planos y puntos en el espacio tridimensional, así como para realizar operaciones matemáticas avanzadas, como la intersección de planos o la distancia entre puntos.

Otra librería útil es la librería `Geometry` que ofrece diversas herramientas para trabajar con geometría en Mathematica. Esta librería proporciona funciones específicas para encontrar puntos de un plano en el espacio tridimensional, así como para realizar cálculos de distancia, ángulos y otras operaciones geométricas.

Además, existen otras librerías especializadas en campos específicos, como la librería `LinearAlgebra`, que proporciona funciones avanzadas para trabajar con matrices y sistemas de ecuaciones lineales. Estas librerías pueden ser utilizadas de manera conjunta para simplificar y agilizar el proceso de encontrar puntos de un plano en Mathematica.

Las librerías adicionales en Mathematica ofrecen una amplia gama de herramientas y funciones que facilitan el trabajo con planos y puntos en el espacio tridimensional. Estas librerías proporcionan funciones específicas para encontrar puntos de un plano, realizar operaciones matemáticas avanzadas y simplificar el proceso de resolución de problemas geométricos. Utilizar estas librerías puede mejorar significativamente la eficiencia y la precisión de los cálculos relacionados con los planos y puntos en Mathematica.

Qué consejos o trucos adicionales podrías ofrecer para realizar cálculos y gráficos de planos en Mathematica de manera más eficiente

Para realizar cálculos y gráficos de planos de manera más eficiente en Mathematica, hay algunos consejos y trucos adicionales que pueden ser útiles.

1. Utiliza las funciones incorporadas de Mathematica:

Mathematica tiene varias funciones incorporadas que pueden ayudarte a realizar cálculos y gráficos de planos de manera más r rápida . Algunas de estas funciones incluyen Plane para representar un plano, Norm para calcular la normal de un vector, y Dot para realizar productos internos.

2. Simplifica tus expresiones:

Si tus expresiones son demasiado complejas, Mathematica puede tardar más tiempo en realizar los cálculos. Para optimizar el rendimiento, intenta simplificar tus expresiones utilizando las funciones Simplify o FullSimplify.

3. Utiliza variables locales:

Si estás realizando cálculos repetitivos, puedes utilizar variables locales para almacenar los resultados intermedios. Esto puede ayudar a reducir el tiempo de cálculo y mejorar la eficiencia de tu código.

4. Aprovecha la paralelización:

Mathematica cuenta con la capacidad de realizar cálculos en paralelo utilizando múltiples núcleos o procesadores. Si tienes acceso a un sistema con varios núcleos, puedes utilizar las funciones Parallelize o ParallelTable para acelerar tus cálculos.

5. Utiliza los recursos disponibles en línea:

Existen numerosos recursos en línea que pueden ayudarte a resolver problemas o responder preguntas relacionadas con el cálculo y graficación de planos en Mathematica. Puedes aprovechar foros, blogs y tutoriales en línea para obtener consejos adicionales y soluciones a problemas específicos.

6. Explora la documentación de Mathematica:

La documentación de Mathematica es un recurso invaluable para aprender sobre todas las funciones y características disponibles. Asegúrate de consultar la documentación oficial de Mathematica y explorar los ejemplos y tutoriales para aprovechar al máximo las capacidades del software.

Con estos consejos y trucos adicionales, podrás realizar cálculos y gráficos de planos de manera más eficiente en Mathematica. Recuerda practicar y experimentar con diferentes funciones y técnicas para mejorar tus habilidades en el software. ¡Buena suerte!

Preguntas frecuentes (FAQ)

1. ¿Cómo puedo encontrar la ecuación de un plano en Mathematica?

Para encontrar la ecuación de un plano en Mathematica, puedes utilizar la función PlaneEquation. Solo debes proporcionarle los puntos que pertenecen al plano y te devolverá la ecuación correspondiente.

2. ¿Qué función puedo utilizar para encontrar la intersección de un plano con otros objetos geométricos en Mathematica?

Puedes utilizar la función RegionIntersection para encontrar la intersección de un plano con otros objetos geométricos en Mathematica. Solo debes proporcionarle el plano y el objeto con el que deseas encontrar la intersección.

3. ¿Cómo puedo graficar un plano en Mathematica?

Para graficar un plano en Mathematica, puedes utilizar la función Graphics3D. Solo debes especificar la ecuación del plano y ajustar los parámetros para obtener la representación visual deseada.

4. ¿Es posible encontrar la distancia entre un punto y un plano en Mathematica?

Sí, es posible encontrar la distancia entre un punto y un plano en Mathematica utilizando la función EuclideanDistance. Solo debes proporcionarle las coordenadas del punto y la ecuación del plano.

5. ¿Qué función puedo utilizar para encontrar el ángulo entre un plano y un vector en Mathematica?

Puedes utilizar la función VectorAngle para encontrar el ángulo entre un plano y un vector en Mathematica. Solo debes proporcionarle la ecuación del plano y las coordenadas del vector.