Cómo calcular la recta normal en un punto con Mathematica

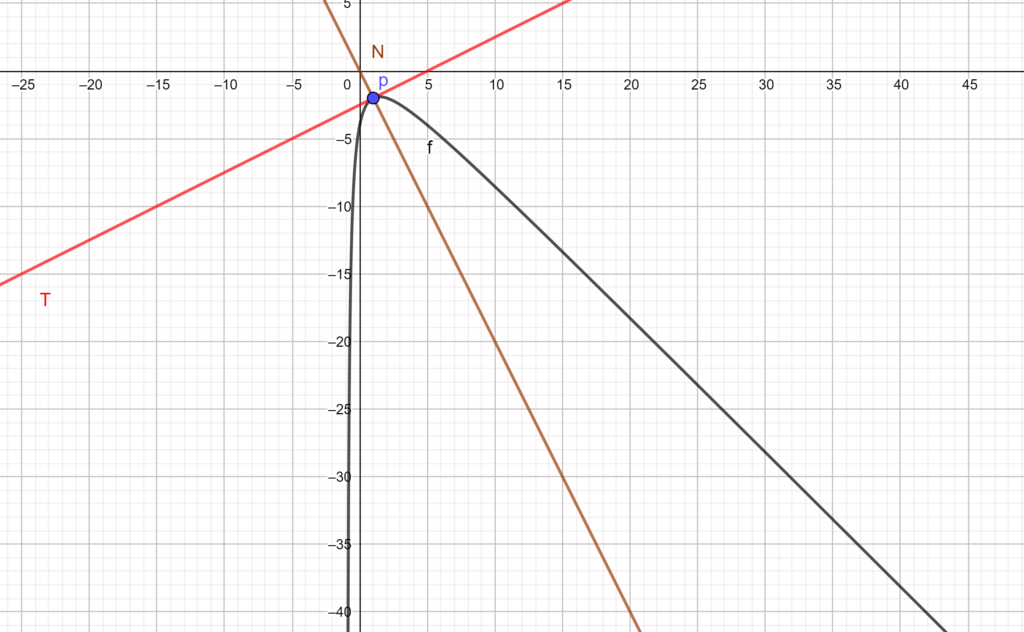
La recta normal es una herramienta fundamental en el cálculo de derivadas, ya que nos permite determinar la pendiente de una función en un punto específico. En términos geométricos, la recta normal es perpendicular a la tangente de la curva en ese punto. En este artículo aprenderemos cómo calcular la recta normal en un punto utilizando el software Mathematica.

Te explicaré paso a paso cómo utilizar Mathematica para calcular la recta normal en un punto. Primero, te mostraré cómo definir la función y el punto en el que quieres calcular la recta normal. Luego, te guiaré a través del proceso de derivación de la función para obtener la pendiente de la recta tangente en ese punto. Por último, te mostraré cómo utilizar la pendiente de la recta tangente para obtener la pendiente de la recta normal y, finalmente, cómo graficar la recta normal en el mismo gráfico que la función original.

Cuál es la definición de la recta normal en matemáticas

En matemáticas, la recta normal se refiere a una línea que es perpendicular a una curva en un punto dado. Se utiliza para determinar la pendiente de la curva en ese punto específico. La pendiente de la recta normal se calcula utilizando cálculo diferencial y puede ser utilizada para varios propósitos, como encontrar la tasa de cambio instantánea o la velocidad en cierto punto de una curva.

En el caso de una función f(x), la pendiente de la recta normal en un punto (a, f(a)) se calcula a través de la derivada de la función evaluada en ese punto. La ecuación de la recta normal se obtiene utilizando la fórmula y - f(a) = f'(a)(x - a).

En el siguiente apartado, te explicaré cómo puedes calcular la recta normal en un punto utilizando el software Mathematica.

Qué es Mathematica y cómo se utiliza para cálculos matemáticos

Mathematica es un software de cálculo matemático que permite realizar una amplia variedad de tareas, desde operaciones básicas hasta análisis complejos. Proporciona una interfaz intuitiva y potente para trabajar con ecuaciones, fórmulas y funciones matemáticas.

Con Mathematica, puedes realizar cálculos numéricos, simbólicos y gráficos de manera eficiente. Es una herramienta muy utilizada en campos como la física, la estadística, la ingeniería y la investigación científica en general.

Para utilizar Mathematica, simplemente debes escribir tus comandos en el lenguaje de programación propio de la herramienta. Este lenguaje es muy versátil y permite realizar una amplia gama de operaciones matemáticas y manipulación de datos.

Una vez que has escrito tus comandos en Mathematica, puedes evaluarlos y obtener resultados inmediatos. Además, puedes guardar tus trabajos y resultados para poder acceder a ellos posteriormente.

Mathematica es una poderosa herramienta de cálculo matemático que te permite realizar una variedad de tareas de manera eficiente y precisa.

Cuál es la fórmula para calcular la pendiente de una recta

La pendiente de una recta se puede calcular utilizando la fórmula m = (y2 - y1) / (x2 - x1). En esta fórmula, (x1, y1) y (x2, y2) son las coordenadas de dos puntos distintos en la recta. La pendiente representa la inclinación de la recta y nos indica cómo cambia la variable dependiente (y) en relación con la variable independiente (x). Un valor positivo de la pendiente indica una recta ascendente, mientras que un valor negativo indica una recta descendente.

Para calcular la pendiente de una recta en un punto específico, necesitamos utilizar el concepto de la recta normal. La recta normal es perpendicular a la recta original y pasa por el punto de interés. La pendiente de la recta normal se puede calcular utilizando la fórmula m_normal = -1 / m_original, donde m_original es la pendiente de la recta original. Esta fórmula nos permite encontrar la pendiente de la recta normal sin necesidad de conocer las coordenadas de otro punto en la recta.

Una vez que tenemos la pendiente de la recta normal, podemos utilizarla junto con las coordenadas del punto de interés para determinar la ecuación de la recta normal. La ecuación de una recta se puede expresar en la forma y = mx + b, donde m es la pendiente y b es el intercepto en el eje y. Sustituyendo la pendiente de la recta normal y las coordenadas del punto de interés en la ecuación, podemos determinar el valor de b. De esta forma, obtenemos la ecuación completa de la recta normal en el punto dado.

Cómo se calcula la pendiente de la recta tangente en un punto

Calcular la pendiente de la recta tangente en un punto es esencial para poder determinar la recta normal en dicho punto. Para hacerlo, utilizaremos el método del límite, que consiste en tomar la derivada de la función en ese punto específico.

La derivada de una función nos da la tasa de cambio instantánea en ese punto, es decir, qué tan rápido está cambiando la función en ese instante. Para calcularla, podemos utilizar la función "D" de Mathematica, que nos dará la derivada exacta de la función en ese punto.

Una vez que tenemos la derivada, evaluamos la función en el punto dado y obtenemos la pendiente de la recta tangente. Esta pendiente nos dará la dirección de la recta normal en ese punto.

Ahora que sabemos cómo calcular la pendiente de la recta tangente en un punto, podemos proceder a determinar la recta normal en dicho punto. La recta normal es perpendicular a la recta tangente y pasa por el punto dado.

Para encontrar la ecuación de la recta normal, utilizaremos la fórmula de la pendiente-intersección, que nos da la ecuación general de una recta. Esta fórmula es de la forma "y = mx + b", donde "m" es la pendiente de la recta y "b" es la intersección con el eje y.

Reemplazando la pendiente de la recta tangente obtenida anteriormente en la fórmula de la pendiente-intersección, obtendremos la ecuación de la recta normal en el punto dado. Podemos utilizar la función "Solve" de Mathematica para despejar la intersección "b" y así obtener la ecuación final.

El cálculo de la pendiente de la recta tangente en un punto es esencial para poder determinar la recta normal en dicho punto. Utilizando la derivada de la función y la fórmula de la pendiente-intersección, podemos calcular la pendiente y la ecuación de la recta normal de manera precisa y eficiente usando Mathematica.

Cuál es la relación entre la pendiente de la recta tangente y la pendiente de la recta normal

La relación entre la pendiente de la recta tangente y la pendiente de la recta normal en un punto de una curva es un concepto fundamental en cálculo diferencial. La pendiente de la recta tangente en un punto representa la tasa de cambio instantánea de la curva en ese punto, mientras que la pendiente de la recta normal es perpendicular a la tangente y se obtiene tomando el recíproco negativo de la pendiente de la tangente. Es decir, si la pendiente de la tangente es m, entonces la pendiente de la recta normal es -1/m.

Esta relación es especialmente útil en el cálculo de la recta normal en un punto utilizando el software Mathematica. Al conocer la pendiente de la tangente en un punto, podemos calcular fácilmente la pendiente de la recta normal usando la fórmula -1/m. A partir de la pendiente de la recta normal y las coordenadas del punto, podemos obtener la ecuación de la recta normal utilizando la conocida ecuación de la recta y = mx + b.

Veamos un ejemplo práctico de cómo calcular la recta normal en un punto utilizando Mathematica:

Cuál es la ecuación de una recta normal a una curva en un punto dado

La recta normal a una curva en un punto dado es una línea recta que es perpendicular a la curva en ese punto específico. Para calcular esta recta normal, necesitamos conocer la ecuación de la curva y el punto en el que queremos encontrar la recta normal.

En el caso de una curva representada por una función matemática, podemos calcular la recta normal utilizando la derivada de la función en el punto dado. La derivada nos da la pendiente de la curva en ese punto, y la pendiente de la recta normal será el negativo inverso de la pendiente de la curva en el punto dado.

Utilizando este conocimiento, podemos calcular la ecuación de la recta normal utilizando la fórmula y - y₁ = m(x - x₁), donde (x₁, y₁) es el punto dado y m es la pendiente de la recta normal.

Cuáles son los pasos para calcular la recta normal utilizando Mathematica

Para calcular la recta normal en un punto utilizando Mathematica, debemos seguir una serie de pasos. En primer lugar, necesitamos determinar las coordenadas del punto en el que queremos calcular la recta normal. Esto lo podemos hacer utilizando las funciones de ingreso de datos de Mathematica. Una vez que tenemos las coordenadas del punto, procedemos a encontrar la derivada de la función que define la curva en ese punto. Mathematica nos ofrece la función "D" para realizar esta operación de manera sencilla y rápida. La derivada nos dará la pendiente de la tangente a la curva, que será la misma pendiente de la recta normal.

Una vez que tenemos la pendiente de la recta normal, necesitamos encontrar la ecuación de la recta que pasa por el punto y tiene esa pendiente. Para ello, utilizamos la ecuación de la recta: y - y1 = m(x - x1), donde m es la pendiente y (x1, y1) son las coordenadas del punto. Mathematica nos permite realizar esta operación utilizando la función "Solve". Finalmente, obtenemos la ecuación de la recta normal en función de x y y, lista para ser utilizada en futuros cálculos.

Existen otros software o herramientas que se pueden utilizar para calcular la recta normal

Además de Mathematica, existen otras herramientas y software que también permiten calcular la recta normal en un punto. Algunos ejemplos son MATLAB, Python con la librería NumPy, y GeoGebra. Estas herramientas son muy populares entre científicos, ingenieros y matemáticos, ya que ofrecen una amplia gama de funcionalidades para resolver problemas matemáticos y realizar cálculos numéricos. Dependiendo de tus necesidades y preferencias personales, podrás elegir la herramienta que mejor se adapte a ti. A continuación, analizaremos brevemente cómo se puede calcular la recta normal en un punto utilizando cada una de estas herramientas.

1. MATLAB

En MATLAB, puedes calcular la recta normal en un punto utilizando la función 'gradient'. Esta función calcula el gradiente de una función en un punto específico. Una vez calculado el gradiente, puedes encontrar la recta normal utilizando la fórmula dada por:

recta_normal = -1/gradient

donde 'gradient' es el valor calculado por la función 'gradient'.

Después de calcular la recta normal, puedes trazarla en el plano utilizando la función 'plot'. Esto te permitirá visualizar la recta normal en relación con la función original.

2. Python con NumPy

En Python, puedes utilizar la librería NumPy para calcular la recta normal en un punto. Para ello, necesitarás importar la librería NumPy y utilizar las funciones 'gradient' y 'plot' de la siguiente manera:

import numpy as np
x = np.linspace(-10, 10, 100)
y = np.sin(x)
gradient = np.gradient(y, x)
recta_normal = -1/gradient
plt.plot(x, y)
plt.plot(x, recta_normal)
plt.show()

Este código generará un gráfico con la función original y la recta normal trazada en el plano.

3. GeoGebra

En GeoGebra, puedes utilizar el comando 'TangentLine' para calcular la recta normal en un punto. Para ello, sigue los siguientes pasos:

1. Define la función original en GeoGebra.
2. Selecciona el punto en el que deseas calcular la recta normal.
3. Escribe el comando 'TangentLine' seguido del punto y la función.
4. GeoGebra generará automáticamente la recta normal en el punto seleccionado.

Además de generar la recta normal, GeoGebra también te permitirá visualizar la función original y la recta normal en el plano.

Calcular la recta normal en un punto es una operación que se puede realizar utilizando diferentes herramientas matemáticas como MATLAB, Python con NumPy y GeoGebra. Cada una de estas herramientas tiene sus propias ventajas y características, por lo que podrás elegir la que mejor se adapte a tus necesidades y conocimientos.

Cuál es la importancia de calcular la recta normal en problemas de optimización y física

Calcular la recta normal es esencial en problemas de optimización y física, ya que nos permite encontrar el punto de máxima o mínima pendiente en una curva. En optimización, la recta normal nos indica la dirección en la que debemos mover un objeto para alcanzar el mínimo o máximo de una función. En física, la recta normal representa la dirección de la fuerza resultante sobre un objeto en movimiento curvilíneo. Por lo tanto, comprender cómo calcular la recta normal es clave para resolver problemas en diversas áreas de estudio.

Concepto de recta normal

La recta normal en un punto de una curva es una línea que pasa por ese punto y es perpendicular a la recta tangente en ese mismo punto. La recta tangente es la línea que toca la curva en ese punto y tiene la misma pendiente que la curva en ese punto. En otras palabras, la recta normal es la línea que "se levanta" de forma perpendicular en el punto donde la curva es más pronunciada.

Cómo calcular la recta normal con Mathematica

Para calcular la recta normal en un punto con Mathematica, podemos utilizar la función "Normal" junto con la función "Slope" (pendiente en inglés). La función "Slope" nos permite obtener la pendiente de la curva en un punto específico y luego, utilizando la función "Normal", podemos obtener la ecuación de la recta normal en ese punto. Veamos un ejemplo:

slope = Slope;
normal = Normal;

Donde "curve" es la curva en la que queremos calcular la recta normal y "point" es el punto donde queremos calcularla. Al ejecutar estas líneas de código, obtendremos la pendiente y la ecuación de la recta normal en el punto especificado.

Aplicaciones de la recta normal

La recta normal es ampliamente utilizada en problemas de optimización y física. En optimización, nos permite encontrar el punto de máxima o mínima pendiente en una curva, lo que es útil en problemas de maximización de ganancias, minimización de costos, entre otros. En física, la recta normal nos ayuda a determinar la dirección de la fuerza resultante sobre un objeto en movimiento curvilíneo, lo que es fundamental para entender el movimiento de los objetos en diferentes situaciones.

Calcular la recta normal es esencial en problemas de optimización y física. Nos permite encontrar el punto de máxima o mínima pendiente en una curva y determinar la dirección de la fuerza resultante en un objeto en movimiento curvilíneo. Con Mathematica, podemos calcular fácilmente la recta normal en un punto mediante las funciones "Slope" y "Normal". El uso de la recta normal tiene aplicaciones prácticas en diversas áreas de estudio y nos ayuda a resolver problemas de manera más eficiente y precisa.

Qué aplicaciones prácticas tiene el cálculo de la recta normal en la vida cotidiana

El cálculo de la recta normal tiene múltiples aplicaciones en la vida cotidiana, especialmente en el campo de la física y la ingeniería. Este concepto es fundamental para comprender el comportamiento de objetos en movimiento, como vehículos en la carretera o proyectiles en el aire.

En el ámbito de la arquitectura y la construcción, el cálculo de la recta normal es esencial para determinar la estabilidad de estructuras, como puentes o edificios, y garantizar su resistencia frente a fuerzas externas.

Además, en la industria del diseño y la animación 3D, el cálculo de la recta normal se utiliza para crear superficies suaves y realistas, aportando un mayor nivel de detalle y precisión a los modelos virtuales.

Comprender y poder calcular la recta normal es fundamental en numerosas áreas de la vida cotidiana, contribuyendo a la seguridad, la eficiencia y la exactitud de diversos procesos y proyectos.

Existen ejemplos o ejercicios de práctica para calcular la recta normal en un punto con Mathematica

En el ámbito de las matemáticas y la programación, es de gran ayuda contar con ejemplos o ejercicios prácticos para entender y aplicar conceptos complejos. En este caso, calcular la recta normal en un punto utilizando Mathematica puede resultar desafiante para algunos. Por suerte, existen varios ejemplos disponibles que permiten practicar y comprender mejor este proceso. Estos ejemplos suelen incluir instrucciones paso a paso, así como el código necesario para ejecutar el cálculo de la recta normal de manera eficiente.

Uno de los ejemplos más comunes es calcular la recta normal en un punto de una función dada. Para ello, se utiliza el comando "Normal" en Mathematica. Este comando permite obtener la recta normal a una curva en un punto específico, facilitando así el cálculo y la representación gráfica de la misma.

Además, también existen ejercicios que combinan la utilización de Mathematica con otros conceptos matemáticos, como derivadas e integrales. Estos ejercicios brindan una mayor comprensión de cómo utilizar Mathematica para calcular la recta normal en diferentes situaciones y cómo aplicar este conocimiento en problemas del mundo real.

¿Dónde encontrar estos ejemplos y ejercicios prácticos?

Existen diversas fuentes en línea donde se pueden encontrar ejemplos y ejercicios prácticos para calcular la recta normal en un punto con Mathematica. Algunas de estas fuentes incluyen:

• Páginas web de tutoriales y documentación de Mathematica
• Foros y comunidades en línea especializadas en matemáticas y programación
• Libros y manuales sobre Mathematica y cálculo diferencial

Estas fuentes suelen proporcionar ejemplos detallados y explicaciones paso a paso para ayudar a los usuarios a comprender y aplicar correctamente el cálculo de la recta normal en un punto utilizando Mathematica.

Beneficios de utilizar ejemplos y ejercicios prácticos

El uso de ejemplos y ejercicios prácticos para calcular la recta normal en un punto con Mathematica ofrece una serie de beneficios, tanto para principiantes como para usuarios más avanzados. Algunos de estos beneficios incluyen:

1. Mejor comprensión de los conceptos matemáticos y su aplicación en la programación
2. Mayor familiaridad con el uso de Mathematica y sus comandos específicos
3. Desarrollo de habilidades de resolución de problemas y pensamiento lógico
4. Mayor confianza al utilizar Mathematica en proyectos y tareas relacionadas con cálculo y matemáticas

Contar con ejemplos y ejercicios prácticos es fundamental para aprender y dominar el cálculo de la recta normal en un punto utilizando Mathematica. Estos recursos proporcionan un enfoque práctico y aplicado a los conceptos teóricos, lo que facilita su comprensión y aplicación en diferentes contextos.

Hay alguna fórmula o método para calcular la recta normal sin utilizar software de matemáticas

Sí, existe una fórmula matemática para calcular la recta normal en un punto sin necesidad de utilizar software de matemáticas. La recta normal es aquella que es perpendicular a la tangente en ese punto de la curva. Para calcularla, se utiliza el concepto de la derivada de una función. La derivada nos dará la pendiente de la tangente en el punto dado. Luego, para obtener la pendiente de la recta normal, simplemente se calcula el negativo inverso de la pendiente de la tangente. Con esta información, se puede determinar la ecuación de la recta normal utilizando la conocida fórmula y-y₁=m(x-x₁).

Sin embargo, utilizar software de matemáticas como Mathematica puede hacer este proceso mucho más sencillo y rápido. Mathematica es una herramienta poderosa que permite realizar cálculos matemáticos complejos de manera eficiente. Con tan solo unos pocos comandos, se puede obtener la ecuación de la recta normal en un punto específico sin necesidad de conocer la fórmula o realizar cálculos manuales.

El primer paso para utilizar Mathematica es definir la función que describe la curva en la que se desea calcular la recta normal. Esto se puede hacer utilizando el comando "Function" seguido de la expresión matemática que define la curva. Por ejemplo, si queremos calcular la recta normal en el punto (2, 4) de la función f(x) = x², podemos definir la función de la siguiente manera:

f := x^2

Luego, utilizamos el comando "D" seguido del nombre de la función y el valor del punto en el que queremos calcular la recta normal. Por ejemplo, para calcular la pendiente de la tangente en el punto (2, 4), utilizamos el siguiente comando:

tangent_slope = D, x] /. x -> 2

Este comando nos dará el valor de la pendiente de la tangente en el punto (2, 4).

Finalmente, utilizamos el comando "ContourPlot" para graficar la curva y la recta normal en el mismo gráfico. Este comando toma como argumentos la función que describe la curva y la ecuación de la recta normal. Por ejemplo, para graficar la función f(x) = x² y la recta normal en el punto (2, 4), utilizamos el siguiente comando:

ContourPlot, tangent_slope(x - 2) + 4}, {x, -5, 5}, PlotRange -> {-10, 10}, Axes -> True]

Este comando generará un gráfico que muestra la curva y la recta normal en el punto dado.

Aunque es posible calcular la recta normal en un punto utilizando una fórmula matemática, el uso de software de matemáticas como Mathematica puede simplificar y agilizar el proceso. Mathematica permite realizar cálculos matemáticos complejos de manera eficiente y ofrece comandos específicos para calcular la recta normal en un punto de una curva. Esto facilita el trabajo y permite obtener resultados precisos en poco tiempo.

Preguntas frecuentes (FAQ)

1. ¿Qué es la recta normal en un punto?

La recta normal en un punto es una línea perpendicular a la curva en ese punto.

2. ¿Cómo puedo calcular la recta normal en un punto con Mathematica?

Para calcular la recta normal en un punto con Mathematica, puedes utilizar la función Normal] donde {x1, y1} son las coordenadas del punto en la curva y {x2, y2} son las coordenadas de un punto cercano a {x1, y1}.

3. ¿Qué es la función Normal en Mathematica?

La función Normal en Mathematica es utilizada para convertir una expresión simbólica a su forma normal. En el caso de calcular la recta normal en un punto, utilizamos la función para obtener la ecuación de la recta normal.

4. ¿Cómo puedo obtener la ecuación de la recta normal en Mathematica?

Para obtener la ecuación de la recta normal en Mathematica, puedes utilizar la función Normal] y luego simplificar la expresión obtenida utilizando la función Simplify.

5. ¿Puedo usar Mathematica para calcular la recta normal en puntos de una curva tridimensional?

Sí, Mathematica puede ser utilizado para calcular la recta normal en puntos de una curva tridimensional utilizando la función Normal]. Solo debes asegurarte de ingresar las coordenadas correctamente.