
Cómo calcular la derivada direccional con precisión en Mathematica
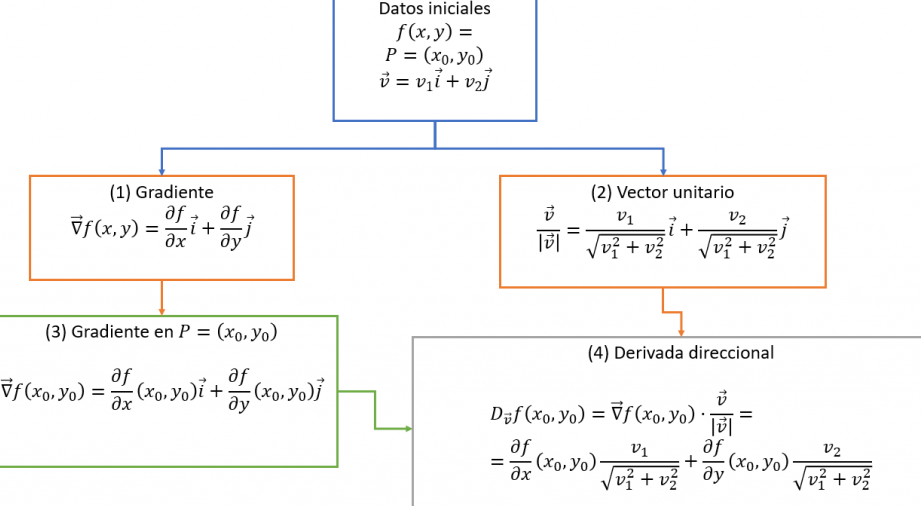
La derivada direccional es un concepto importante en el cálculo multivariable, que permite determinar cómo cambia una función en una dirección específica. Es especialmente útil en campos como la física, la ingeniería y la economía, donde la variación de una magnitud en una dirección particular es relevante. En Mathematica, un software matemático ampliamente utilizado, se pueden realizar cálculos precisos de derivadas direccionales utilizando algunas funciones y comandos específicos.
Exploraremos cómo calcular la derivada direccional con precisión en Mathematica. Veremos paso a paso cómo utilizar los comandos adecuados y cómo interpretar los resultados obtenidos. También analizaremos algunas aplicaciones prácticas de la derivada direccional y cómo puede ser útil en diferentes contextos. Si estás interesado en el cálculo de derivadas direccionales y quieres aprender a hacerlo de manera precisa en Mathematica, ¡sigue leyendo!
- Cuál es la fórmula para calcular la derivada direccional en Mathematica
- Cómo puedo encontrar la dirección óptima para calcular la derivada direccional en un punto específico
- Cuál es la importancia de la derivada direccional en el análisis de funciones
- Es posible calcular la derivada direccional en puntos donde la función no es diferenciable
- Cuáles son las limitaciones y suposiciones al calcular la derivada direccional en Mathematica
- Existen funciones predefinidas en Mathematica para calcular la derivada direccional
- Cuál es la relación entre la derivada direccional y la pendiente de una curva en un punto dado
- Cómo puedo representar gráficamente la derivada direccional en Mathematica
- Cuál es la interpretación geométrica de la derivada direccional
- Cómo puedo utilizar la derivada direccional para optimizar funciones en Mathematica
- Cuál es la diferencia entre la derivada direccional y la derivada parcial de una función en Mathematica
- Cuáles son las aplicaciones prácticas de la derivada direccional en campos como la física y la economía
- Existen casos en los que no se puede calcular la derivada direccional en Mathematica
- Cuál es el orden de complejidad computacional al calcular la derivada direccional en Mathematica
-
Preguntas frecuentes (FAQ)
- 1. ¿Qué es la derivada direccional?
- 2. ¿Cómo se calcula la derivada direccional en Mathematica?
- 3. ¿Qué significa la precisión en el cálculo de la derivada direccional?
- 4. ¿Cómo puedo especificar la precisión en el cálculo de la derivada direccional en Mathematica?
- 5. ¿Cuál es la ventaja de calcular la derivada direccional con precisión en Mathematica?
Cuál es la fórmula para calcular la derivada direccional en Mathematica
La derivada direccional es una herramienta matemática utilizada para calcular la tasa de cambio de una función en una dirección específica. En Mathematica, calcular la derivada direccional es bastante sencillo gracias a las funciones incorporadas en el software.
La fórmula para calcular la derivada direccional en Mathematica es:
Derivativef
Donde vec es un vector de dirección en el espacio tridimensional y f es la función de la que se desea calcular la derivada. Esta fórmula puede adaptarse para funciones de cualquier número de variables mediante la adecuada indexación del vector de dirección.
Veamos un ejemplo para una función en dos variables:
Cómo puedo encontrar la dirección óptima para calcular la derivada direccional en un punto específico
En matemáticas, la derivada direccional se utiliza para calcular la tasa de cambio de una función en una dirección particular. Para encontrar la dirección óptima, puedes utilizar el software Mathematica, que ofrece una amplia gama de herramientas para realizar cálculos matemáticos de manera precisa.
Para calcular la derivada direccional en un punto específico en Mathematica, primero debes definir la función en la que deseas calcular la derivada. Puedes hacerlo utilizando la función "f:= ..." seguido de la expresión de la función. Por ejemplo, si deseas encontrar la derivada direccional de la función f(x, y) = x^2 + y^2 en el punto (2, 1), puedes escribir:
f := x^2 + y^2
A continuación, debes especificar la dirección en la que deseas calcular la derivada. Puedes hacerlo utilizando un vector dirección. Por ejemplo, si deseas calcular la derivada direccional en la dirección ⟨1, -1⟩, puedes escribir:
direction = {1, -1}
Luego, puedes utilizar la función Grad para calcular el gradiente de la función en el punto especificado. El gradiente te dará la dirección de máxima tasa de cambio de la función. Para calcular el gradiente, puedes escribir:
gradient = Grad, {x, y}] /. {x -> 2, y -> 1}
A continuación, puedes utilizar la función Normalize para normalizar el vector de dirección. Esto asegurará que la dirección tenga una longitud de 1 y mantenga la misma dirección. Para normalizar el vector de dirección, puedes escribir:
normalizedDirection = Normalize
Una vez que hayas calculado el gradiente y normalizado el vector de dirección, puedes calcular la derivada direccional utilizando la fórmula:
directionalDerivative = gradient . normalizedDirection
Finalmente, puedes evaluar la derivada direccional en el punto especificado sustituyendo los valores adecuados en la expresión. En este caso, puedes escribir:
directionalDerivative /. {x -> 2, y -> 1}
Al ejecutar este código en Mathematica, obtendrás el valor numérico de la derivada direccional en la dirección óptima.
Cuál es la importancia de la derivada direccional en el análisis de funciones
La derivada direccional es una herramienta fundamental en el análisis de funciones, ya que nos permite medir la tasa de cambio de una función en una dirección específica. Esto es especialmente útil en campos como la física, la economía y la ingeniería, donde es necesario comprender cómo una función varía en relación a diferentes variables.
Al calcular la derivada direccional, podemos determinar la pendiente de la función en una dirección particular, lo que nos brinda información valiosa sobre cómo se comporta la función en ese punto específico.
En definitiva, la derivada direccional nos ayuda a entender mejor el comportamiento de una función y nos permite realizar análisis más precisos y detallados.
Es posible calcular la derivada direccional en puntos donde la función no es diferenciable
Uno de los desafíos en el cálculo de la derivada direccional es que solo se puede calcular en puntos donde la función es diferenciable. Sin embargo, en Mathematica, es posible calcular la derivada direccional incluso en puntos donde la función no es diferenciable.
Esto es posible gracias a la potente capacidad de cálculo simbólico de Mathematica. La función DirectionalDerivative permite calcular la derivada direccional en cualquier punto de una función, sin importar si es diferenciable o no.
Para calcular la derivada direccional en un punto donde la función no es diferenciable, simplemente se especifica el vector dirección deseado y el punto en el que se desea calcular la derivada. Mathematica realiza los cálculos necesarios utilizando técnicas avanzadas de cálculo simbólico.
Esta capacidad de Mathematica es extremadamente útil en situaciones donde se necesita calcular la tasa de cambio de una función en un punto específico, incluso si la función no es diferenciable en ese punto. Esto amplía significativamente las aplicaciones prácticas del cálculo diferencial.
Cuáles son las limitaciones y suposiciones al calcular la derivada direccional en Mathematica
Al calcular la derivada direccional en Mathematica, es importante tener en cuenta ciertas limitaciones y suposiciones. Primero, se asume que la función subyacente es diferenciable en el punto de interés. Esto significa que la función debe tener derivadas parciales bien definidas en ese punto.
Otra limitación es que se trabaja con aproximaciones numéricas, por lo que siempre hay cierto grado de error asociado. La precisión de los cálculos depende de factores como la tolerancia establecida y el tamaño de los incrementos utilizados.
Además, la precisión de las derivadas direccionales también puede verse afectada por la forma en que se elige el vector dirección. Cuanto más cercano esté el vector a la dirección de máximo cambio, mayor será la precisión. Sin embargo, elegir la dirección correcta puede ser un desafío, ya que puede no ser evidente cuál es la dirección óptima en cada caso.
Aunque Mathematica ofrece una herramienta poderosa para calcular derivadas direccionales, es necesario tener en cuenta las limitaciones inherentes y las suposiciones realizadas para obtener resultados precisos.
Existen funciones predefinidas en Mathematica para calcular la derivada direccional
Mathematica, el potente software de matemáticas, ofrece una gama de funciones predefinidas que facilitan el cálculo de la derivada direccional. Estas funciones permiten obtener resultados precisos y confiables en un tiempo mínimo.
Una de las funciones más utilizadas para este propósito es la función DirDerivative. Esta función toma dos argumentos: la función de interés y el vector dirección en el que se desea calcular la derivada. Con solo unos pocos pasos, puedes obtener fácilmente el valor de la derivada direccional con una alta precisión.
Otra función útil es la función NumericQ, que se utiliza para evaluar la derivada direccional en un punto específico. Esta función le permite especificar el punto de evaluación y obtener un resultado numérico en poco tiempo.
Además de estas funciones predefinidas, también puedes utilizar operadores como el operador Grad para calcular la derivada direccional en Mathematica. Este operador toma la función de interés y el vector dirección como argumentos y devuelve el valor de la derivada en el punto especificado.
Cuál es la relación entre la derivada direccional y la pendiente de una curva en un punto dado
La derivada direccional y la pendiente de una curva en un punto dado están estrechamente relacionadas. La derivada direccional mide la tasa de cambio instantánea de una función en una dirección particular, mientras que la pendiente de una curva en un punto dado representa la inclinación de la curva en ese punto.
En otras palabras, la derivada direccional te permite calcular la tasa de cambio en una dirección específica, mientras que la pendiente de una curva te da información sobre la pendiente instantánea de la curva en un punto dado.
Para calcular la derivada direccional en Mathematica, es necesario utilizar el concepto de gradiente y la dirección en la cual se desea calcular la tasa de cambio. Esto se logra mediante el uso de la función "ND", que representa una derivada direccional numérica.
Por otro lado, la pendiente de una curva en un punto dado se calcula mediante el uso del concepto de derivada. En Mathematica, se puede utilizar la función "D" para calcular la derivada de una función y obtener así la pendiente de la curva en un punto específico.
Tanto la derivada direccional como la pendiente de una curva en un punto dado son herramientas poderosas para estudiar la tasa de cambio y la inclinación de una función. En Mathematica, se pueden calcular con precisión utilizando las funciones "ND" y "D", respectivamente.
Cómo puedo representar gráficamente la derivada direccional en Mathematica
En Mathematica, puedes representar gráficamente la derivada direccional utilizando la función "VectorPlot". Esta función te permite visualizar el vector gradiente y la dirección en la que se calcula la derivada direccional. Primero, debes definir la función en la que deseas calcular la derivada direccional utilizando la notación de funciones de Mathematica. Luego, especificas el punto de evaluación y la dirección en la que deseas calcular la derivada. Utiliza la opción "VectorScale" para ajustar el tamaño de los vectores y "VectorStyle" para personalizar su apariencia. Finalmente, utiliza "Show" para mostrar la gráfica junto con cualquier otro gráfico que desees agregar.
Por ejemplo, supongamos que deseas calcular la derivada direccional de la función f(x,y) = x^2 + y^2 en el punto (1,1) en la dirección (1,1). Puedes hacerlo de la siguiente manera:
f := x^2 + y^2;
punto = {1, 1};
direccion = {1, 1};
A continuación, utiliza la función "VectorPlot" para representar gráficamente la derivada direccional:
VectorPlot, x], D, y]}.direccion, {x, -2, 2}, {y, -2, 2}, VectorScale -> 0.2, VectorStyle -> Arrowheads]
Esto generará una gráfica que muestra los vectores de la derivada direccional en el punto (1,1) en la dirección (1,1). Puedes ajustar los parámetros de "VectorScale" y "VectorStyle" según tus preferencias.
Recuerda que la derivada direccional representa la tasa de cambio de la función en una dirección específica. Utilizando Mathematica, puedes visualizar fácilmente esta información y obtener una representación gráfica precisa.
Cuál es la interpretación geométrica de la derivada direccional
La derivada direccional es una medida de cómo cambia una función en una dirección específica en un punto dado. Geométricamente, se puede pensar como la pendiente de la tangente a la curva de nivel en ese punto. Es decir, indica la tasa de cambio de la función en la dirección de un vector unitario dado.
La derivada direccional se puede calcular utilizando el gradiente de la función y un vector unitario que representa la dirección deseada. Esta medida es útil en muchos campos, como la física, la economía y la ingeniería, ya que proporciona información sobre cómo cambia una función en una dirección particular.
En el contexto de Mathematica, es posible calcular la derivada direccional con precisión utilizando las herramientas y funciones adecuadas. A continuación, veremos cómo hacerlo paso a paso.
Cómo puedo utilizar la derivada direccional para optimizar funciones en Mathematica
La optimización de funciones es una tarea común en muchas áreas de la ciencia y la ingeniería. Una técnica útil para maximizar o minimizar funciones es utilizar la derivada direccional. En Mathematica, podemos calcular la derivada direccional de una función en un punto dado utilizando la función 'D'. La sintaxis es la siguiente:
DerivativeDirectional, {x, y}, {h, k}]
Donde 'f' es la función de interés, '{x, y}' son las variables independientes, y '{h, k}' es el vector dirección. La derivada direccional nos da la tasa de cambio instantánea de la función en la dirección especificada.
Para maximizar o minimizar una función utilizando la derivada direccional, podemos encontrar los puntos donde la derivada direccional es igual a cero o cambia de signo. Esto se puede lograr utilizando métodos numéricos o simbólicos en Mathematica.
La derivada direccional es una herramienta poderosa para optimizar funciones en Mathematica. Nos permite encontrar los máximos y mínimos locales, lo que puede ser útil en la resolución de problemas de optimización en diversas áreas.
Cuál es la diferencia entre la derivada direccional y la derivada parcial de una función en Mathematica
En Mathematica, la derivada direccional y la derivada parcial son dos conceptos importantes en el cálculo de funciones. La derivada parcial se refiere a la tasa de cambio de una función en una variable específica, mientras que la derivada direccional se refiere a la tasa de cambio en una dirección específica.
La principal diferencia entre estas dos derivadas radica en la dirección en la que se calcula la tasa de cambio. La derivada parcial se calcula manteniendo constantes todas las variables excepto la variable de interés, y se obtiene la tasa de cambio con respecto a esa variable. Por otro lado, la derivada direccional se calcula a lo largo de una dirección específica, lo que significa que todas las variables pueden cambiar simultáneamente.
La derivada parcial mide la tasa de cambio en una dirección específica, mientras que la derivada direccional mide la tasa de cambio en una dirección arbitraria.
Cuáles son las aplicaciones prácticas de la derivada direccional en campos como la física y la economía
La derivada direccional es una herramienta fundamental en campos como la física y la economía. En física, se utiliza para calcular la tasa de cambio de una magnitud en una dirección específica, lo que permite analizar el movimiento de partículas en trayectorias curvas. En economía, la derivada direccional se emplea para medir el impacto de cambios en variables fundamentales como la oferta y la demanda, facilitando el análisis de cómo estas variables afectan el equilibrio en los mercados. La derivada direccional es esencial para comprender y predecir los cambios en sistemas complejos en diversos campos de estudio.
Existen casos en los que no se puede calcular la derivada direccional en Mathematica
Aunque Mathematica es una herramienta poderosa para calcular derivadas, existen casos en los que no es posible calcular la derivada direccional con precisión. Esto ocurre cuando la función no es diferenciable en algún punto o si la dirección no está bien definida.
Por ejemplo, si la función tiene una discontinuidad en el punto de interés, la derivada direccional no se puede calcular de manera exacta. En estos casos, se puede utilizar una aproximación numérica para obtener un valor aproximado de la derivada direccional.
La dirección también juega un papel importante en el cálculo de la derivada direccional. Si la dirección no está bien definida, como por ejemplo en el caso de una función multivariable con múltiples mínimos locales, la derivada direccional puede no existir.
Es importante tener en cuenta estas limitaciones al calcular la derivada direccional en Mathematica, y utilizar herramientas adicionales cuando sea necesario para obtener resultados precisos y confiables.
Cuál es el orden de complejidad computacional al calcular la derivada direccional en Mathematica
La derivada direccional es una herramienta comúnmente utilizada en análisis numérico y cálculo para estudiar la variación de una función en una dirección particular. En Mathematica, calcular la derivada direccional es un proceso relativamente sencillo gracias a la extensa biblioteca de funciones matemáticas disponibles.
En términos de complejidad computacional, el cálculo de la derivada direccional en Mathematica tiene un orden de complejidad lineal, es decir, O(n), donde n es el número de variables independientes en la función. Esto significa que el tiempo de ejecución del cálculo aumenta de manera proporcional al número de variables independientes.
Es importante tener en cuenta que el rendimiento computacional puede verse afectado por la complejidad del cálculo de la función subyacente y los métodos numéricos utilizados. En general, Mathematica es altamente optimizado para cálculos matemáticos y ofrece diversas opciones para mejorar la precisión y eficiencia de los cálculos de derivadas direccionales.
Pasos para calcular la derivada direccional en Mathematica
Para calcular la derivada direccional en Mathematica, se deben seguir los siguientes pasos:
- Definir la función a partir de la cual se calculará la derivada direccional.
- Especificar el punto en el cual se evaluará la derivada direccional.
- Definir el vector dirección en el cual se calculará la derivada direccional.
- Utilizar la función
DirectionalDerivativede Mathematica para obtener el valor numérico de la derivada direccional.
Es importante destacar que Mathematica permite trabajar con funciones simbólicas, lo que significa que se pueden realizar cálculos exactos en lugar de aproximaciones numéricas. Esto proporciona una mayor precisión en los cálculos de derivadas direccionales.
Preguntas frecuentes (FAQ)
1. ¿Qué es la derivada direccional?
La derivada direccional es la tasa de cambio instantánea de una función en una dirección específica.
2. ¿Cómo se calcula la derivada direccional en Mathematica?
En Mathematica, puedes utilizar la función "D" junto con la dirección deseada para calcular la derivada direccional.
3. ¿Qué significa la precisión en el cálculo de la derivada direccional?
La precisión se refiere al nivel de exactitud deseado en el cálculo de la derivada direccional. Una mayor precisión significa un resultado más preciso, pero también puede requerir más tiempo de cálculo.
4. ¿Cómo puedo especificar la precisión en el cálculo de la derivada direccional en Mathematica?
Para especificar la precisión en Mathematica, puedes utilizar la opción "WorkingPrecision" junto con el valor deseado. Por ejemplo, "WorkingPrecision -> 10".
5. ¿Cuál es la ventaja de calcular la derivada direccional con precisión en Mathematica?
Calcular la derivada direccional con precisión en Mathematica te permite obtener resultados más confiables y precisos en tus cálculos, lo cual es especialmente útil en situaciones donde la precisión es crítica, como en aplicaciones científicas y técnicas.
Deja una respuesta







Artículos que podrían interesarte