Aprende fácilmente a simular un péndulo doble en Wolfram Mathematica

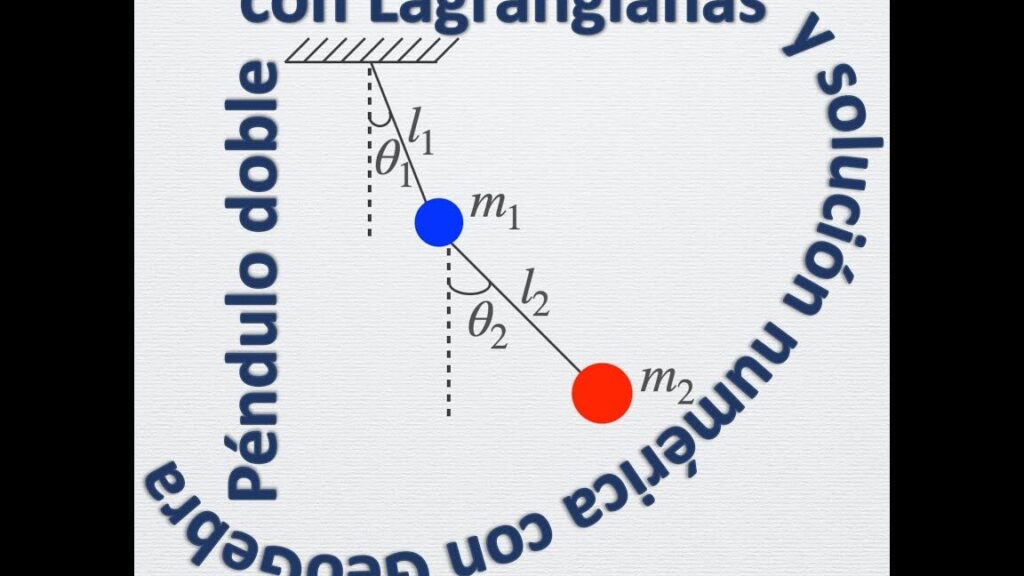
El péndulo doble es un sistema físico interesante y desafiante de estudiar. Consiste en dos péndulos conectados en serie, lo que le confiere un comportamiento complejo y no lineal. Este sistema presenta una rica variedad de movimientos, incluyendo oscilaciones regulares, caos y estados estables. Simular y analizar el comportamiento de un péndulo doble puede ser útil en campos como la física, la ingeniería y la robótica.

Te enseñaré cómo simular un péndulo doble utilizando el software Wolfram Mathematica. Veremos cómo definir las ecuaciones de movimiento, cómo resolverlas numéricamente y cómo visualizar los resultados. También exploraremos algunas variaciones interesantes del péndulo doble, como introducir fuerzas externas y analizar el comportamiento en diferentes condiciones iniciales. ¡Prepárate para sumergirte en el fascinante mundo del péndulo doble!

Cuál es la definición de un péndulo doble y cómo se diferencia de un péndulo simple

La oscilación caótica es un fenómeno en el cual el movimiento de un sistema no sigue un patrón predecible a largo plazo y es altamente sensible a las condiciones iniciales. En el caso del péndulo doble, este comportamiento caótico puede surgir debido a la presencia de múltiples modos de oscilación.

La existencia de múltiples modos de oscilación en el péndulo doble significa que hay diferentes formas en las que los péndulos pueden moverse en el mismo plano. Estos modos de oscilación pueden interactuar entre sí y producir un comportamiento complejo y aparentemente aleatorio.

Cuando se observa un péndulo doble en un estado de oscilación caótica, puede parecer que los péndulos se mueven de manera impredecible y desordenada. Sin embargo, a pesar de la aparente falta de regularidad en el movimiento, aún hay ciertas características del sistema que se mantienen constantes.

Por ejemplo, el péndulo doble conserva la energía total del sistema, lo que significa que la suma de las energías cinética y potencial en cualquier momento dado se mantiene constante. Sin embargo, la forma en que se distribuye esta energía entre los diferentes modos de oscilación puede cambiar de manera caótica a medida que el sistema evoluciona en el tiempo.

Otro aspecto interesante de la oscilación caótica en el péndulo doble es que el sistema exhibe una fuerte dependencia de las condiciones iniciales. Esto significa que una pequeña variación en las posiciones o velocidades iniciales de los péndulos puede dar lugar a trayectorias completamente diferentes en el espacio de fase.

El espacio de fase es una representación gráfica que muestra cómo evoluciona el sistema a lo largo del tiempo. En el caso del péndulo doble, el espacio de fase tiene dos dimensiones, una para cada coordenada generalizada del sistema. Las trayectorias caóticas en el espacio de fase pueden ocupar regiones grandes y complicadas, lo que refleja la naturaleza impredecible del movimiento del péndulo doble.

Cuáles son las aplicaciones prácticas de simular un péndulo doble en Wolfram Mathematica

Simular un péndulo doble en Wolfram Mathematica puede tener aplicaciones prácticas en varios campos. Por ejemplo, en física, esta simulación puede ayudar a comprender el comportamiento de sistemas mecánicos complejos, como los péndulos dobles que se encuentran en relojes de pared o en dispositivos de suspensión.

Además, esta simulación también puede ser útil en ingeniería, ya que permite analizar las vibraciones y oscilaciones de estructuras como puentes colgantes o grúas de carga.

En el campo de la robótica, simular un péndulo doble en Wolfram Mathematica puede ayudar a diseñar y optimizar sistemas de control para robots que requieren movimientos precisos y estables.

Asimismo, en el ámbito académico y educativo, esta simulación puede ser una herramienta didáctica poderosa para ilustrar principios físicos y matemáticos, así como para enseñar a los estudiantes sobre la importancia de la modelización en la resolución de problemas.

Cómo se pueden modelar las ecuaciones de movimiento de un péndulo doble en Wolfram Mathematica

Simular un péndulo doble puede ser un desafío interesante para aquellos que desean explorar las ecuaciones de movimiento en física. Con la ayuda de Wolfram Mathematica, es posible modelar y visualizar las trayectorias del péndulo doble de manera sencilla y precisa.

Para comenzar, es necesario definir las ecuaciones de movimiento del sistema. El péndulo doble consta de dos masas suspendidas una debajo de la otra, cada una de ellas con su propio ángulo y longitud. Estos ángulos y longitudes son variables que deben ser especificadas en el código.

Una vez definidas las variables, Wolfram Mathematica ofrece funciones y comandos específicos para calcular y representar las trayectorias del péndulo doble. Por ejemplo, la función "NDSolve" permite resolver numéricamente las ecuaciones diferenciales que describen el movimiento del sistema.

Además de la simulación del movimiento del péndulo doble, también es posible graficar otras variables interesantes, como la energía total del sistema. Esto brinda una visión más completa de cómo evoluciona el sistema a lo largo del tiempo.

Wolfram Mathematica es una herramienta poderosa para simular y analizar el movimiento de un péndulo doble. Con la combinación adecuada de ecuaciones y comandos, es posible visualizar las trayectorias del sistema con gran precisión y obtener información valiosa sobre su comportamiento.

Qué métodos numéricos se pueden utilizar para simular un péndulo doble en Wolfram Mathematica

Existen varios métodos numéricos que se pueden utilizar para simular un péndulo doble en Wolfram Mathematica. Algunos de los métodos más comunes incluyen:

Método del Euler

El método del Euler es el más simple de implementar. Consiste en aproximar la solución mediante una serie de pasos discretos. Sin embargo, este método tiende a acumular errores y puede no ser muy preciso.

Método del punto medio

El método del punto medio mejora la precisión del método del Euler al utilizar una aproximación más precisa de la derivada en cada paso. Este método suele ser más preciso que el método del Euler, pero aún puede acumular errores en simulaciones largas.

Método de Runge-Kutta

El método de Runge-Kutta es uno de los métodos numéricos más utilizados para simular sistemas dinámicos. Este método utiliza una aproximación de varias etapas para calcular la solución en cada paso. Es más preciso que los métodos anteriores y puede minimizar la acumulación de errores.

Hay varios métodos numéricos disponibles para simular un péndulo doble en Wolfram Mathematica. La elección del método dependerá de la precisión deseada y la eficiencia computacional requerida.

Cuáles son los pasos para simular un péndulo doble en Wolfram Mathematica

Simular un péndulo doble en Wolfram Mathematica puede parecer complicado al principio, pero con los pasos correctos, puedes aprender fácilmente a hacerlo. Aquí te guiaré a través de los pasos necesarios para simular un péndulo doble usando esta herramienta.

Paso 1: Definición de las variables

Antes de comenzar la simulación, debes definir las variables necesarias. En este caso, necesitarás definir las longitudes de los dos brazos del péndulo, así como las masas de cada brazo.

Paso 2: Configuración de las ecuaciones del movimiento

Una vez que hayas definido las variables, deberás configurar las ecuaciones del movimiento para el péndulo doble. Estas ecuaciones se basan en las leyes de Newton y te permitirán simular el comportamiento del sistema.

Paso 3: Integración numérica

Para simular el péndulo doble, necesitarás realizar una integración numérica de las ecuaciones del movimiento. Wolfram Mathematica proporciona herramientas para realizar esta integración de manera sencilla.

Paso 4: Representación gráfica

Una vez que hayas realizado la integración numérica, el siguiente paso es representar gráficamente los resultados de la simulación. Puedes utilizar las funciones de visualización de Wolfram Mathematica para crear gráficos interactivos del péndulo doble en movimiento.

Paso 5: Análisis de resultados

Por último, es importante analizar los resultados de la simulación. Puedes observar cómo cambian las posiciones y velocidades de los brazos del péndulo en función del tiempo, así como analizar otras propiedades del sistema.

Siguiendo estos pasos podrás simular fácilmente un péndulo doble en Wolfram Mathematica. Recuerda que la práctica es fundamental para adquirir un mayor conocimiento sobre la simulación de sistemas físicos utilizando esta herramienta.

Qué parámetros se pueden ajustar para variar el comportamiento del péndulo doble en la simulación de Wolfram Mathematica

En la simulación del péndulo doble en Wolfram Mathematica, existen varios parámetros que se pueden ajustar para variar su comportamiento. Estos parámetros incluyen la longitud de los dos hilos, las masas de las dos partículas, las posiciones iniciales, las velocidades iniciales y la gravedad.

La longitud de los hilos determina la separación entre las partículas y afecta directamente la amplitud de las oscilaciones. Cuanto más largos sean los hilos, mayor será la amplitud de los movimientos del péndulo doble.

Las masas de las partículas también juegan un papel importante. Si las masas son desiguales, el péndulo doble puede oscilar de manera asimétrica, lo que resulta en movimientos más complejos. Por otro lado, si las masas son iguales, el péndulo doble puede moverse de manera más simétrica.

Las posiciones iniciales y las velocidades iniciales determinan la configuración inicial del péndulo doble. Cambiar estas condiciones iniciales puede resultar en diferentes trayectorias y comportamientos del péndulo doble durante la simulación.

Por último, la gravedad es otro parámetro ajustable. Aumentar o disminuir la gravedad afectará la velocidad y la aceleración del péndulo doble, lo que puede llevar a cambios significativos en su movimiento.

Cómo se pueden obtener gráficos y visualizaciones realistas de la simulación de un péndulo doble en Wolfram Mathematica

La simulación de un péndulo doble es una excelente manera de comprender los conceptos detrás de los sistemas físicos complejos. Wolfram Mathematica ofrece una poderosa herramienta para realizar estas simulaciones de manera fácil y efectiva.

Para comenzar, en Mathematica puedes definir las ecuaciones de movimiento del péndulo doble utilizando su lenguaje de programación. Esto te permite obtener resultados precisos y detallados de la simulación.

Una vez que hayas definido las ecuaciones, puedes utilizar las funciones de visualización en Mathematica para crear gráficos que representen el movimiento del péndulo doble en tiempo real. Esto te permitirá observar cómo cambia su posición y velocidad a lo largo del tiempo.

Además, Mathematica te ofrece una amplia variedad de herramientas de personalización para mejorar tus gráficos y visualizaciones. Puedes ajustar el color, el grosor de las líneas y agregar etiquetas para facilitar la comprensión de los resultados.

Además de las visualizaciones en tiempo real, Mathematica también te permite realizar análisis numéricos y obtener resultados cuantitativos de la simulación del péndulo doble. Esto puede ser útil para estudiar el comportamiento del sistema en diferentes condiciones iniciales o para comparar la respuesta de diferentes configuraciones de péndulo.

Wolfram Mathematica es una herramienta poderosa y versátil para simular y visualizar sistemas físicos complejos como el péndulo doble. Con su lenguaje de programación y sus funciones de visualización, puedes obtener resultados precisos y detallados que te ayudarán a comprender mejor este fenómeno físico fascinante.

Qué herramientas adicionales están disponibles en Wolfram Mathematica para analizar y estudiar el comportamiento del péndulo doble

Wolfram Mathematica ofrece varias herramientas poderosas para analizar y estudiar el comportamiento del péndulo doble. Una de las más útiles es la función NDSolve, que nos permite resolver numéricamente las ecuaciones diferenciales que describen el movimiento del péndulo.

Además, Mathematica también proporciona funciones para visualizar los resultados de la simulación del péndulo doble. Podemos utilizar la función ParametricPlot para trazar la trayectoria del péndulo en el espacio fase, o la función Animate para crear una animación del movimiento del péndulo en tiempo real.

Otra herramienta interesante es la función Manipulate, que nos permite interactuar con los parámetros del péndulo doble y observar cómo cambia su movimiento en tiempo real. Esto es especialmente útil para comprender cómo diferentes valores de masa, longitud y ángulo inicial afectan el comportamiento del péndulo.

También podemos utilizar Mathematica para calcular energía y otros parámetros del péndulo doble a lo largo del tiempo. Esto nos permite estudiar cómo se conserva la energía total del sistema y cómo se distribuye entre las diferentes formas de energía (cinética y potencial).

Wolfram Mathematica ofrece una amplia gama de herramientas y funciones para analizar y estudiar el comportamiento del péndulo doble. Ya sea que estemos interesados en la simulación numérica, la visualización gráfica o el análisis de energía, Mathematica tiene todo lo que necesitamos para explorar este fascinante sistema físico.

Cuáles son los desafíos comunes al simular un péndulo doble en Wolfram Mathematica y cómo se pueden superar

La simulación de un péndulo doble en Wolfram Mathematica puede presentar algunos desafíos. Uno de ellos es la complejidad matemática involucrada en la modelización del movimiento del péndulo y la interacción entre las dos masas. Esto requiere un conocimiento sólido de las ecuaciones diferenciales y la física del movimiento oscilatorio.

Otro desafío es la visualización de los resultados. Mientras que Mathematica ofrece muchas herramientas para la visualización de datos, representar gráficamente el movimiento del péndulo doble puede resultar complicado. Es importante encontrar una representación clara y comprensible que muestre tanto las posiciones como las velocidades de las masas en función del tiempo.

Además, es esencial asegurarse de la precisión numérica de la simulación. Esto implica elegir los métodos de integración adecuados y establecer correctamente los parámetros de tiempo y paso de integración. Una mala elección de estos parámetros puede llevar a resultados inexactos o incluso a errores numéricos en la simulación.

Finalmente, otro desafío común es la optimización del código. Para simular un péndulo doble de manera eficiente, es importante utilizar técnicas de programación eficientes y aprovechar al máximo las capacidades de paralelización de Mathematica. Esto permitirá reducir el tiempo de cómputo y aumentar la velocidad de la simulación.

Simular un péndulo doble en Wolfram Mathematica puede ser desafiante debido a la complejidad matemática, la visualización de los resultados, la precisión numérica y la optimización del código. Sin embargo, con el conocimiento adecuado y las técnicas correctas, estos desafíos pueden superarse con éxito.

Cómo se puede utilizar la simulación de un péndulo doble en Wolfram Mathematica para explorar fenómenos físicos en otros campos de estudio

La simulación de un péndulo doble en Wolfram Mathematica no solo es una herramienta útil para comprender los fundamentos de la física, sino que también puede aplicarse en otros campos de estudio. Por ejemplo, en biología se pueden utilizar modelos de péndulo doble para simular el movimiento de articulaciones en organismos vivos. Esto permite explorar cómo se pueden producir movimientos fluidos y eficientes en animales y humanos.

En la astrofísica, la simulación de péndulos dobles ha demostrado ser útil para entender la dinámica de sistemas de múltiples estrellas. Estos modelos pueden ayudar a predecir la evolución de sistemas estelares y estudiar las interacciones gravitacionales complejas entre los cuerpos celestes.

En el campo de la ingeniería, la simulación de péndulos dobles puede aplicarse para analizar la estabilidad y el comportamiento de estructuras colgantes, como puentes o grúas. Estos modelos permiten evaluar cómo diferentes factores, como la longitud de los cables o la masa de los objetos suspendidos, afectan la respuesta del sistema y ayudan a diseñar estructuras más seguras y eficientes.

Además, la simulación de péndulos dobles en Wolfram Mathematica es una herramienta valiosa para la enseñanza y el aprendizaje de conceptos físicos complejos. Los estudiantes pueden interactuar con los modelos y experimentar con diferentes parámetros para observar cómo afectan el comportamiento del sistema. Esto facilita la comprensión de conceptos abstractos y fomenta un enfoque más práctico y visual del aprendizaje.

Ventajas de utilizar Wolfram Mathematica para simular un péndulo doble

Existen recursos o tutoriales en línea para aprender más sobre la simulación de un péndulo doble en Wolfram Mathematica

Si estás interesado en aprender a simular un péndulo doble en Wolfram Mathematica, estás de suerte. Hay una gran cantidad de recursos y tutoriales en línea que te pueden ayudar a dominar esta tarea. A través de estos recursos, podrás aprender los conceptos básicos de la simulación de un péndulo doble, así como entender cómo utilizar las funciones y herramientas específicas de Wolfram Mathematica para llevar a cabo esta simulación.

Uno de los recursos más populares para aprender sobre la simulación de un péndulo doble en Wolfram Mathematica es el sitio web oficial de Wolfram. Aquí encontrarás una amplia gama de documentación, guías y tutoriales que te guiarán paso a paso en el proceso de creación y simulación de un péndulo doble. Desde conceptos básicos hasta técnicas más avanzadas, este recurso te proporcionará toda la información necesaria para que puedas dominar esta simulación en poco tiempo.

También existen tutoriales en video disponibles en plataformas como YouTube

Si prefieres aprender de forma visual, también puedes encontrar una variedad de tutoriales en video sobre la simulación de un péndulo doble en Wolfram Mathematica en plataformas como YouTube. Estos tutoriales te mostrarán en tiempo real cómo utilizar las funciones y herramientas específicas de Wolfram Mathematica para crear y simular un péndulo doble. Además, muchos de estos tutoriales también proporcionan ejemplos prácticos y consejos útiles para mejorar tus habilidades de simulación.

Además de los recursos en línea, también puedes considerar unirte a comunidades en línea y foros de discusión dedicados a Wolfram Mathematica. Estas comunidades son excelentes lugares para hacer preguntas, compartir tus propias simulaciones de péndulo doble y obtener comentarios y consejos de otros entusiastas y expertos en el campo. Puedes encontrar estas comunidades en plataformas como Stack Exchange o Reddit.

Si estás interesado en aprender a simular un péndulo doble en Wolfram Mathematica, hay una gran cantidad de recursos disponibles en línea. Ya sea a través del sitio web oficial de Wolfram, tutoriales en video o comunidades en línea, podrás encontrar toda la información y el apoyo que necesitas para dominar esta tarea. Así que no esperes más, ¡comienza tu viaje de aprendizaje hoy mismo!

Preguntas frecuentes (FAQ)

1. ¿Qué es un péndulo doble?

Un péndulo doble es un sistema físico compuesto por dos péndulos simples conectados entre sí, lo que hace que su movimiento sea más complejo y desafiante de analizar.

2. ¿Por qué es importante simular un péndulo doble?

La simulación de un péndulo doble permite comprender mejor los principios físicos que rigen su movimiento, así como explorar diferentes condiciones iniciales y observar cómo afectan el comportamiento del sistema.

3. ¿Cuál es la utilidad de usar Wolfram Mathematica para simular un péndulo doble?

Wolfram Mathematica es una poderosa herramienta de cálculo y simulación que facilita la programación y visualización de sistemas físicos complejos como el péndulo doble. Además, ofrece una amplia gama de funciones y gráficos que ayudan a analizar los resultados de la simulación.

4. ¿Es necesario tener conocimientos avanzados de programación para simular un péndulo doble en Mathematica?

No es necesario tener conocimientos avanzados de programación para simular un péndulo doble en Mathematica. Existen recursos y ejemplos disponibles en la documentación oficial de Mathematica, así como tutoriales en línea, que te guiarán paso a paso en el proceso de simulación.

5. ¿Qué tipos de análisis se pueden realizar con la simulación de un péndulo doble?

La simulación de un péndulo doble permite realizar análisis cualitativos y cuantitativos del sistema, como el estudio de trayectorias, periodos y energía del sistema, así como la observación de transiciones entre diferentes modos de movimiento, entre otros.