Aprende a hacer planos de fases en Wolfram Mathematica: guía completa

Además, puedes personalizar los estilos de las trayectorias usando las opciones "Arrowheads" y "ArrowSize". Por ejemplo, puedes hacer que las flechas sean más grandes y tengan una cabeza más puntiaguda usando la opción "Arrowheads -> {{0.03, 0.8}}".

Si deseas añadir más detalles a las trayectorias, también puedes utilizar la opción "Epilog". Esto te permite agregar elementos adicionales, como puntos, líneas o texto, a los gráficos de las trayectorias.

Personalizar los colores y estilos de las trayectorias en un plano de fases en Wolfram Mathematica es posible utilizando las opciones "PlotStyle", "Arrowheads" y "ArrowSize". Además, puedes añadir más detalles utilizando la opción "Epilog". Con estas herramientas, puedes crear visualizaciones únicas y atractivas de tus trayectorias en Wolfram Mathematica.

Es posible agregar anotaciones y etiquetas a un plano de fases en Wolfram Mathematica

Una de las ventajas de utilizar Wolfram Mathematica es la posibilidad de agregar anotaciones y etiquetas a los planos de fases. Estas anotaciones permiten resaltar puntos importantes, hacer referencia a características específicas o destacar regiones de interés en el diagrama.

Para agregar una anotación, simplemente necesitas utilizar la función Annotate. Esta función acepta como argumentos la posición en el plano de fases donde se colocará la anotación y el texto que se mostrará. Por ejemplo, si quieres agregar una anotación en el punto (2, 3) con el texto "Punto crítico", puedes utilizar la siguiente línea de código:

Annotate

Además de las anotaciones, también puedes utilizar etiquetas para resaltar regiones en el plano de fases. Las etiquetas se crean utilizando la función Text. Esta función acepta como argumentos la posición en el plano de fases donde se colocará la etiqueta y el texto que se mostrará. Por ejemplo, si quieres agregar una etiqueta en el punto (1, 2) con el texto "Región de estabilidad", puedes utilizar la siguiente línea de código:

Text

Al utilizar anotaciones y etiquetas en los planos de fases de Wolfram Mathematica, podrás resaltar puntos relevantes y facilitar la interpretación de tus diagramas.

Qué tipos de sistemas de ecuaciones diferenciales se pueden representar en un plano de fases en Wolfram Mathematica

En Wolfram Mathematica, puedes representar en un plano de fases diversos tipos de sistemas de ecuaciones diferenciales. Estos sistemas pueden ser lineales o no lineales, autónomos o no autónomos, de primer orden o de orden superior. Los sistemas lineales son aquellos cuyas ecuaciones son de la forma dy/dx = ax + by + c, donde a, b y c son constantes. Los sistemas no lineales son aquellos en los que las ecuaciones no siguen esta forma lineal.

Los sistemas autónomos son aquellos en los que las ecuaciones no dependen de la variable independiente, es decir, las ecuaciones son de la forma dy/dt = f(y), donde t es la variable independiente. Los sistemas no autónomos son aquellos en los que las ecuaciones dependen explícitamente de la variable independiente, es decir, las ecuaciones son de la forma dy/dx = f(x, y).

Además, en un plano de fases también se pueden representar sistemas de ecuaciones diferenciales de orden superior, es decir, sistemas en los que las ecuaciones involucran derivadas de orden superior. Estos sistemas requieren un enfoque más avanzado, ya que el número de variables y ecuaciones es mayor, pero Wolfram Mathematica es una herramienta poderosa que puede manejar estos casos de manera eficiente.

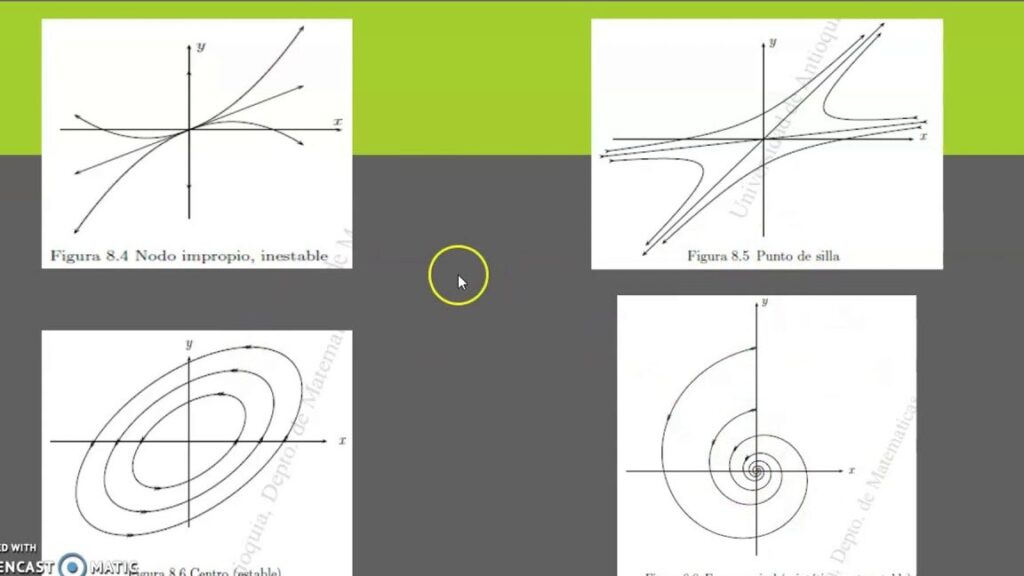
Cuál es la relación entre los puntos críticos y las trayectorias en un plano de fases en Wolfram Mathematica

En un plano de fases en Wolfram Mathematica, los puntos críticos juegan un papel fundamental en la comprensión de las trayectorias de un sistema dinámico. Los puntos críticos son aquellos en los que el vector de campo es nulo, lo que significa que la derivada del sistema con respecto al tiempo es cero en esos puntos.

Estos puntos son importantes porque representan los puntos de equilibrio o estabilidad del sistema. Si un punto crítico es un punto de equilibrio, entonces todas las trayectorias cercanas a él convergerán hacia ese punto a medida que el tiempo tiende a infinito. Por otro lado, si el punto crítico es inestable, las trayectorias se alejarán de ese punto a medida que el tiempo avanza.

Para visualizar estas trayectorias en un plano de fases en Wolfram Mathematica, puedes utilizar la función StreamPlot. Esta función te permitirá trazar las líneas de campo que representan las trayectorias del sistema. Al especificar las condiciones iniciales del sistema, podrás observar cómo evolucionan las trayectorias a lo largo del tiempo.

Un ejemplo práctico

Supongamos que tienes un sistema descrito por las ecuaciones diferenciales:

x' = y
y' = -x

Para trazar las trayectorias en el plano de fases, primero debes definir estas ecuaciones diferenciales utilizando la función NDSolve. A continuación, puedes utilizar la función StreamPlot para trazar las líneas de campo correspondientes a las trayectorias del sistema.

Por ejemplo, si quieres trazar las trayectorias para valores iniciales de x = 1 y y = 0, puedes utilizar el siguiente código:

Es posible animar un plano de fases en Wolfram Mathematica para mostrar la evolución temporal de un sistema de ecuaciones diferenciales

En Wolfram Mathematica, es posible animar un plano de fases para mostrar la evolución temporal de un sistema de ecuaciones diferenciales. Esto puede ser útil para visualizar el comportamiento de un sistema dinámico y comprender mejor sus propiedades y características.

Para crear un plano de fases animado en Wolfram Mathematica, primero necesitamos definir las ecuaciones diferenciales que describen el sistema. Estas ecuaciones pueden ser simples o complejas, dependiendo del sistema que estemos estudiando. Podemos utilizar la función "NDSolve" para resolver las ecuaciones y obtener las soluciones numéricas.

Una vez que tenemos las soluciones numéricas, podemos crear una animación utilizando la función "Animate" de Mathematica. Dentro de la animación, podemos representar el plano de fases utilizando la función "ParametricPlot" y agregar información adicional, como flechas de dirección o puntos de equilibrio.

Además de la animación, también es posible agregar controles deslizantes para ajustar los parámetros del sistema y ver cómo afectan el comportamiento del plano de fases. Esto puede ser especialmente útil para explorar diferentes configuraciones y comprender mejor el sistema en estudio.

Wolfram Mathematica ofrece herramientas poderosas para crear planos de fases animados y visualizar la evolución temporal de sistemas de ecuaciones diferenciales. Estas visualizaciones pueden ser de gran ayuda para comprender y analizar sistemas dinámicos en diversas áreas, como física, química, biología y economía.

Existen recursos y tutoriales adicionales para aprender a crear planos de fases en Wolfram Mathematica

Si estás interesado en aprender a crear planos de fases en Wolfram Mathematica, estás de suerte. Existen muchos recursos y tutoriales disponibles tanto en línea como en libros especializados que te pueden ayudar a dominar esta técnica.

Una de las mejores formas de aprender es a través de tutoriales en video. Hay muchos canales de YouTube dedicados a Wolfram Mathematica que tienen excelentes tutoriales paso a paso sobre cómo crear planos de fases. Estos videos son ideales para aquellos que prefieren aprender viendo en acción.

Además de los tutoriales en video, también puedes encontrar varios libros sobre Wolfram Mathematica que cubren la creación de planos de fases. Estos libros suelen incluir explicaciones detalladas, ejemplos de código y ejercicios prácticos para que puedas practicar y mejorar tus habilidades.

Otro recurso valioso son los foros en línea y las comunidades de Wolfram Mathematica. Estos lugares son ideales para hacer preguntas, obtener ayuda y conectarse con otros usuarios que también están interesados en crear planos de fases. Puedes encontrar respuestas a tus preguntas, compartir tus propios proyectos y aprender de la experiencia de otras personas.

Si estás interesado en aprender a hacer planos de fases en Wolfram Mathematica, hay una amplia gama de recursos disponibles para ti. Ya sea que prefieras tutoriales en video, libros o foros en línea, puedes encontrar el método de aprendizaje que mejor se adapte a tus necesidades. Recuerda practicar regularmente y experimentar con diferentes ejemplos para desarrollar tus habilidades en la creación de planos de fases.

Preguntas frecuentes (FAQ)

1. ¿Qué es un plano de fases en Wolfram Mathematica?

Un plano de fases en Wolfram Mathematica es una representación gráfica que muestra las trayectorias de un sistema dinámico en función de sus variables. Es una herramienta útil para analizar el comportamiento del sistema y visualizar las soluciones de las ecuaciones diferenciales.

2. ¿Cómo puedo crear un plano de fases en Wolfram Mathematica?

Para crear un plano de fases en Wolfram Mathematica, debes definir las ecuaciones diferenciales del sistema utilizando la función NDSolve. Luego, utiliza la función ParametricPlot para visualizar las trayectorias del sistema en el plano de fases. Puedes personalizar la apariencia del gráfico utilizando diferentes opciones gráficas.

3. ¿Necesito conocimientos previos en programación para hacer planos de fases en Wolfram Mathematica?

Si bien tener conocimientos previos en programación puede ser útil, no es necesario para hacer planos de fases en Wolfram Mathematica. El software proporciona una interfaz intuitiva y herramientas específicas para crear gráficos de manera sencilla. Sin embargo, familiarizarse con la sintaxis básica de Mathematica puede facilitar el proceso.

4. ¿Cuál es la utilidad de los planos de fases en la física y la ingeniería?

Los planos de fases son herramientas poderosas para visualizar y comprender el comportamiento de sistemas dinámicos en física y ingeniería. Permiten analizar el movimiento de partículas, la estabilidad de sistemas, el comportamiento de circuitos eléctricos, entre otros. Son especialmente útiles para estudiar sistemas con múltiples variables.

5. ¿Dónde puedo encontrar ejemplos de planos de fases en Wolfram Mathematica?

Existen numerosos recursos en línea donde puedes encontrar ejemplos de planos de fases en Wolfram Mathematica. Puedes visitar la página oficial de Wolfram Mathematica, foros y comunidades en línea dedicadas a esta herramienta, y tutoriales en video que te guiarán en la creación de planos de fases paso a paso. También puedes explorar el código fuente de otros proyectos para obtener inspiración.