Aprende a hacer ecuaciones matriciales en Mathematica

Mathematica es un software de cálculo matemático ampliamente utilizado en campos de la ciencia, la ingeniería y las matemáticas. Una de las características más poderosas de Mathematica es su capacidad para trabajar con matrices y resolver ecuaciones matriciales. Esto es especialmente útil para problemas que involucran sistemas de ecuaciones lineales, donde se busca encontrar las soluciones de las variables involucradas.

Exploraremos cómo hacer ecuaciones matriciales en Mathematica y veremos ejemplos prácticos que ilustran su uso. Aprenderemos cómo definir matrices, realizar operaciones básicas como la suma y la multiplicación de matrices, y resolver sistemas de ecuaciones lineales mediante la inversión de matrices. Además, descubriremos cómo utilizar funciones adicionales de Mathematica que nos permiten encontrar los valores y vectores propios de una matriz y calcular su determinante. Si estás interesado en el álgebra lineal y quieres aprender cómo aplicarlo en Mathematica, ¡este artículo es para ti!

Cuáles son las ventajas de utilizar ecuaciones matriciales en Mathematica

Las ecuaciones matriciales en Mathematica nos brindan una forma poderosa y eficiente de representar, manipular y resolver sistemas de ecuaciones lineales. Su uso nos permite ahorrar tiempo y esfuerzo al simplificar y agilizar la resolución de problemas matemáticos y científicos. Una de las ventajas de utilizar ecuaciones matriciales es que nos permite manipular, transformar y resolver sistemas de ecuaciones de manera más rápida y sencilla.

Además, las ecuaciones matriciales nos permiten representar de forma compacta y elegante sistemas de ecuaciones lineales, lo que facilita su comprensión y análisis. Esto es especialmente útil en problemas que involucran grandes cantidades de ecuaciones y variables.

Otra ventaja de utilizar ecuaciones matriciales en Mathematica es que nos permite aplicar operaciones como multiplicación de matrices, cálculo de la inversa y determinante de una matriz, entre otros. Estas operaciones matriciales son fundamentales en muchos campos, como el álgebra lineal, la física y la estadística.

Cómo se representan las matrices en Mathematica

En Mathematica, las matrices se representan utilizando la función "MatrixForm". Esta función toma como argumento una lista de listas, donde cada lista representa una fila de la matriz. Por ejemplo, la matriz A = se representaría en Mathematica de la siguiente manera:

MatrixForm

Una vez que la matriz está representada en Mathematica, podemos realizar diferentes operaciones matriciales, como sumar, restar, multiplicar, transponer, entre otras. Es importante recordar que las matrices en Mathematica son sensibles a las dimensiones y deben tener el mismo número de filas y columnas para poder realizar ciertas operaciones.

Cuáles son las operaciones básicas que se pueden realizar con matrices en Mathematica

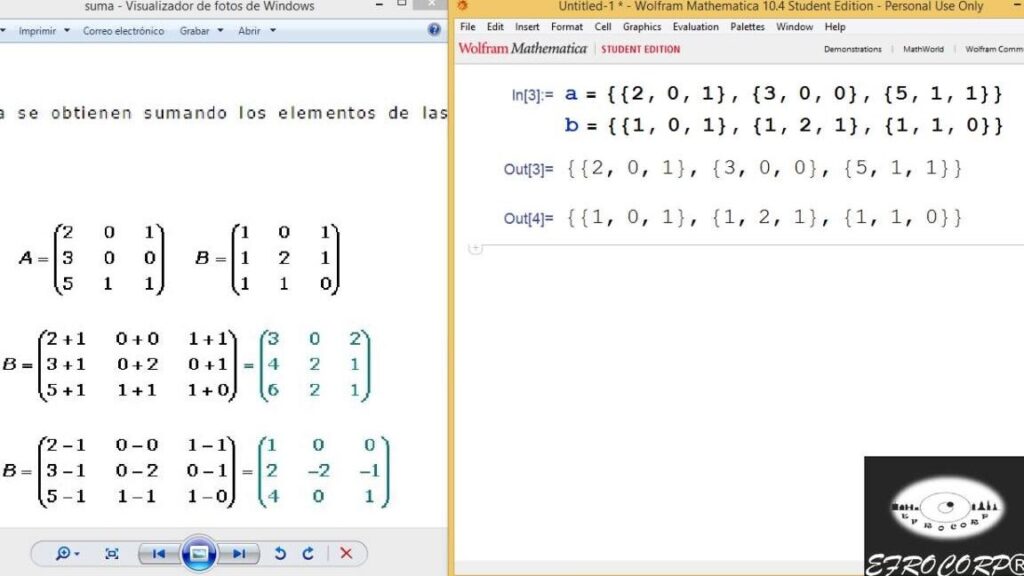
En Mathematica, es posible realizar diversas operaciones básicas con matrices. Una de ellas es la suma de matrices, donde los elementos correspondientes de cada matriz se suman entre sí. Para realizar esta operación, se utiliza el símbolo de suma (+).

Otra operación básica es la multiplicación de matrices. Para multiplicar dos matrices, se utilizan los símbolos de multiplicación (). Es importante tener en cuenta que el número de columnas de la primera matriz debe coincidir con el número de filas de la segunda matriz.

Además de la suma y la multiplicación, también se puede realizar la transposición de una matriz en Mathematica. La transposición cambia las filas por columnas y viceversa. Para transponer una matriz, se utiliza la función Transpose.

Suma de matrices en Mathematica

Para sumar dos matrices en Mathematica, simplemente se utilizan los símbolos de suma (+). Por ejemplo, si tenemos dos matrices A y B, la operación de suma se realiza de la siguiente manera: C = A + B.

Es importante tener en cuenta que las matrices deben tener las mismas dimensiones para poder sumarse. Si las matrices tienen dimensiones diferentes, Mathematica mostrará un error.

Podemos ilustrar esto con un ejemplo. Supongamos que tenemos las siguientes matrices:

A = {{1, 2, 3}, {4, 5, 6}}
B = {{7, 8, 9}, {10, 11, 12}}

Entonces, la suma de estas matrices se realizaría de la siguiente manera:

C = A + B

El resultado sería:

{{8, 10, 12}, {14, 16, 18}}

Multiplicación de matrices en Mathematica

La multiplicación de matrices en Mathematica se realiza utilizando los símbolos de multiplicación (). Por ejemplo, si tenemos dos matrices A y B, la operación de multiplicación se realiza de la siguiente manera: C = A B.

Es importante tener en cuenta que el número de columnas de la primera matriz debe coincidir con el número de filas de la segunda matriz para que la multiplicación sea posible. Si no se cumple esta condición, se mostrará un error.

Veamos un ejemplo de multiplicación de matrices. Supongamos que tenemos las siguientes matrices:

A = {{1, 2}, {3, 4}}
B = {{5, 6}, {7, 8}}

Entonces, la multiplicación de estas matrices se realizaría de la siguiente manera:

C = A B

El resultado sería:

{{19, 22}, {43, 50}}

Transposición de matrices en Mathematica

En Mathematica, la transposición de una matriz se realiza utilizando la función Transpose. Esta función cambia las filas por columnas y viceversa.

Por ejemplo, si tenemos la matriz A, podemos obtener su transpuesta de la siguiente manera:

A = {{1, 2, 3}, {4, 5, 6}}
B = Transpose

El resultado sería:

{{1, 4}, {2, 5}, {3, 6}}

La transposición de una matriz puede ser útil en diversas aplicaciones, como el cálculo de determinantes o la resolución de sistemas de ecuaciones lineales.

Cómo se resuelve un sistema de ecuaciones matriciales en Mathematica

Resolver un sistema de ecuaciones matriciales en Mathematica es una tarea sencilla gracias a su potente lenguaje de programación y las funciones específicas para trabajar con matrices. Para resolver un sistema de ecuaciones matriciales, simplemente debemos definir las matrices y utilizar la función LinearSolve.

A continuación, se muestra un ejemplo de cómo resolver un sistema de ecuaciones matriciales en Mathematica:

A = {{1, 2}, {3, 4}};
B = {5, 6};
X = LinearSolve;
X

En este ejemplo, se define la matriz A como una matriz de 2x2 y la matriz B como un vector de 2 elementos. Luego, se utiliza la función LinearSolve para obtener la solución del sistema de ecuaciones matriciales y se guarda en la variable X.

Una vez que tenemos la solución, podemos obtener los valores de las incógnitas o realizar operaciones adicionales con la matriz solución.

Resolver un sistema de ecuaciones matriciales en Mathematica es tan sencillo como definir las matrices y utilizar la función LinearSolve. Esta poderosa herramienta facilita el trabajo con matrices y simplifica la resolución de sistemas de ecuaciones matriciales.

Cuál es la sintaxis para ingresar una ecuación matricial en Mathematica

En Mathematica, para ingresar una ecuación matricial, debes utilizar la función "Array" seguida de los valores de la matriz. Por ejemplo, si deseas ingresar una matriz de 2x2, puedes escribir Array(a, {2, 2}). Esto creará una matriz con las variables a11, a12, a21 y a22. También puedes ingresar valores específicos en la matriz utilizando la misma sintaxis, por ejemplo, Array({1, 2, 3, 4}, {2, 2}) creará una matriz con los valores 1, 2, 3 y 4.

Además de la función "Array", Mathematica también ofrece otras funciones para trabajar con matrices, como "IdentityMatrix" para generar una matriz identidad, "Transpose" para transponer una matriz y "Dot" para realizar multiplicación matricial. Estas funciones te ayudarán a realizar cálculos y operaciones matriciales de manera sencilla y eficiente.

Una vez ingresada la ecuación matricial, puedes utilizar las funciones de Mathematica para resolver sistemas de ecuaciones lineales, encontrar autovalores y autovectores, diagonalizar matrices, entre otras operaciones matriciales. ¡Explora las posibilidades que te ofrece Mathematica y lleva tus cálculos matriciales al siguiente nivel!

Existen funciones predefinidas en Mathematica para simplificar el cálculo de ecuaciones matriciales

Mathematica es un potente software de matemáticas que ofrece numerosas funciones predefinidas para simplificar el cálculo de ecuaciones matriciales. Estas funciones permiten realizar operaciones básicas como la suma, la resta y la multiplicación de matrices, así como el cálculo de determinantes, valores propios y eigenvectores.

Para realizar cualquier operación con matrices en Mathematica, se utiliza la función "MatrixForm", la cual permite visualizar las matrices de manera clara y organizada. Además, Mathematica ofrece la posibilidad de realizar operaciones de manera simbólica, lo que facilita el cálculo y simplifica los resultados.

Operaciones básicas con matrices

En Mathematica, las matrices se definen utilizando corchetes y separando los elementos de cada fila por comas. Por ejemplo:


A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}


Una vez definidas las matrices, se pueden realizar operaciones básicas como suma y resta utilizando los operadores "+" y "-". Por ejemplo:


B = {{1, 1, 1}, {1, 1, 1}, {1, 1, 1}}
C = A + B
D = A - B


Además de las operaciones básicas, Mathematica permite realizar la multiplicación de matrices mediante la función "Dot". Por ejemplo:


E = A.Dot


También es posible calcular la traspuesta de una matriz utilizando la función "Transpose". Por ejemplo:


F = Transpose


Cálculo de determinantes, valores propios y eigenvectores

Mathematica ofrece funciones específicas para calcular el determinante de una matriz, así como los valores propios y eigenvectores. Para calcular el determinante de una matriz, se utiliza la función "Det". Por ejemplo:


detA = Det


Para calcular los valores propios de una matriz, se utiliza la función "Eigenvalues". Por ejemplo:


valoresPropios = Eigenvalues


Para calcular los eigenvectores de una matriz, se utiliza la función "Eigenvectors". Por ejemplo:


eigenVectores = Eigenvectors


Estas funciones son de gran utilidad cuando se trabaja con ecuaciones matriciales y permiten simplificar los cálculos, ahorrando tiempo y evitando posibles errores.

Se pueden realizar operaciones elementales de filas y columnas en Mathematica

Una de las ventajas de utilizar Mathematica es que permite realizar operaciones elementales de filas y columnas en matrices. Estas operaciones son útiles cuando se desean simplificar o resolver sistemas de ecuaciones lineales. Por ejemplo, se pueden intercambiar filas o columnas, multiplicar una fila o columna por una constante, o sumar o restar una fila o columna a otra. Todo esto se puede realizar de forma sencilla utilizando las funciones y operadores proporcionados por Mathematica.

Para intercambiar filas o columnas en una matriz, se puede utilizar la función ReplacePart. Por ejemplo, para intercambiar la primera fila con la segunda fila de una matriz A, se puede utilizar la siguiente expresión: A = ReplacePart],2->A]}]. Esto reemplaza el elemento en la posición 1 de la matriz A con la segunda fila de la matriz, y el elemento en la posición 2 de la matriz A con la primera fila de la matriz.

Para multiplicar una fila o columna por una constante, se puede utilizar la función Times o el operador . Por ejemplo, para multiplicar la segunda fila de una matriz A por un factor de 2, se puede utilizar la siguiente expresión: A = ReplacePart]}]. Esto multiplica la segunda fila de la matriz A por 2.

Para sumar o restar una fila o columna a otra, se puede utilizar la función Plus o Minus, respectivamente. Por ejemplo, para sumar la segunda fila de una matriz A a la primera fila, se puede utilizar la siguiente expresión: A = ReplacePart]+A]}]. Esto suma la segunda fila de la matriz A a la primera fila.

Estas operaciones elementales son muy útiles al realizar manipulaciones y cálculos con matrices en Mathematica. Permiten simplificar matrices y resolver sistemas de ecuaciones lineales de manera eficiente y precisa. Es importante tener en cuenta que estas operaciones se pueden aplicar a matrices de cualquier dimensión y con cualquier valor numérico o simbólico.

Es posible calcular la inversa de una matriz en Mathematica

En Mathematica es posible calcular la inversa de una matriz utilizando la función Inverse. Esta función toma como argumento la matriz que deseamos invertir y devuelve la matriz inversa correspondiente. Es importante tener en cuenta que no todas las matrices son invertibles, es decir, algunas matrices no tienen inversa. En estos casos, Mathematica devolverá un error. Sin embargo, si la matriz es invertible, podremos utilizar la matriz inversa en cálculos posteriores, como multiplicarla por un vector para resolver un sistema de ecuaciones lineales.

Para calcular la inversa de una matriz en Mathematica, simplemente escribimos el nombre de la matriz seguido de Inverse. Por ejemplo, si tenemos una matriz llamada A, podemos calcular su inversa de la siguiente manera: Inverse. Mathematica devolverá la matriz inversa correspondiente. Es importante destacar que es recomendable utilizar matrices numéricas y evitar el uso de matrices simbólicas, ya que el cálculo de la inversa puede ser más complejo en estos casos.

Una vez que hemos calculado la inversa de una matriz, podemos utilizarla en cálculos posteriores. Por ejemplo, podemos multiplicar la matriz inversa por un vector para resolver un sistema de ecuaciones lineales. Para hacer esto, utilizamos el operador . (punto) en Mathematica. Por ejemplo, si tenemos una matriz inversa A_inv y un vector b, podemos resolver el sistema de ecuaciones lineales Ax = b de la siguiente manera: x = A_inv.b. Mathematica realizará la multiplicación y devolverá el vector solución x.

Cuál es la forma más eficiente de resolver ecuaciones matriciales grandes en Mathematica

Resolver ecuaciones matriciales grandes en Mathematica puede ser un desafío. Afortunadamente, existen algunas técnicas que pueden ayudarte a optimizar el proceso y obtener resultados más rápidos y eficientes.

Una forma de resolver ecuaciones matriciales en Mathematica es utilizando la función LinearSolve. Esta función permite resolver sistemas de ecuaciones lineales de forma rápida y sencilla.

Otra técnica útil es descomponer la matriz en sus factores primos. Esto puede facilitar la resolución de ecuaciones matriciales grandes, ya que reduces la complejidad del problema. Puedes utilizar las funciones LUDecomposition o QRDecomposition para realizar esta descomposición.

Además, es importante tener en cuenta la capacidad de procesamiento de tu computadora. Si estás trabajando con matrices muy grandes, es posible que necesites utilizar un equipo con mayor poder de procesamiento o aprovechar la capacidad de procesamiento en paralelo de Mathematica utilizando la función Parallelize.

Otra técnica útil es utilizar operaciones en paralelo para acelerar los cálculos. Mathematica permite realizar operaciones en paralelo utilizando la función ParallelMap o ParallelTable, lo que puede reducir significativamente el tiempo de cálculo.

Finalmente, es recomendable utilizar las opciones de optimización de Mathematica para acelerar los cálculos. Puedes utilizar la función Compile para compilar tu código y obtener un rendimiento óptimo. También puedes ajustar los parámetros de rendimiento utilizando las opciones de CompilationOptions y RuntimeOptions.

Resolver ecuaciones matriciales grandes en Mathematica puede ser un desafío, pero hay varias técnicas que puedes utilizar para optimizar el proceso y obtener resultados más rápidos y eficientes. Utiliza funciones como LinearSolve y técnicas como la descomposición de matrices, aprovecha la capacidad de procesamiento en paralelo, utiliza operaciones en paralelo y ajusta las opciones de optimización para obtener un mejor rendimiento.

Qué recursos adicionales existen para aprender a utilizar ecuaciones matriciales en Mathematica

Si quieres aprender a utilizar ecuaciones matriciales en Mathematica, hay una gran variedad de recursos adicionales que pueden ser de gran ayuda. Una opción es buscar tutoriales en línea que te guíen paso a paso en el proceso de resolver ecuaciones matriciales utilizando este software. También puedes consultar libros especializados en Mathematica, los cuales suelen incluir ejemplos prácticos y explicaciones detalladas sobre el tema. Otra alternativa es unirte a comunidades en línea de usuarios de Mathematica, donde podrás intercambiar conocimientos, hacer preguntas y obtener ayuda de otros usuarios con más experiencia en el tema. Además, algunos sitios web ofrecen cursos en línea sobre el uso de ecuaciones matriciales en Mathematica, que te permitirán adquirir conocimientos de manera más estructurada y profunda.

En cuanto a los recursos gratuitos, puedes explorar la documentación oficial de Mathematica, donde encontrarás ejemplos y explicaciones detalladas sobre el uso de ecuaciones matriciales. Por otro lado, existen foros de discusión en línea donde podrás plantear tus dudas y obtener respuestas de la comunidad de usuarios de Mathematica. Además, muchas universidades y centros de investigación tienen sitios web donde comparten materiales educativos y tutoriales sobre el uso de Mathematica en diferentes áreas, incluyendo ecuaciones matriciales. Por último, no olvides consultar el canal oficial de Wolfram en YouTube, donde encontrarás videos tutoriales sobre Mathematica y su aplicación en diferentes áreas, incluyendo el manejo de ecuaciones matriciales.

Si quieres aprender a utilizar ecuaciones matriciales en Mathematica, existen múltiples recursos adicionales a tu disposición. Ya sea a través de tutoriales en línea, libros especializados, cursos en línea, comunidades de usuarios o recursos gratuitos como la documentación oficial, foros de discusión y canales de YouTube, podrás adquirir conocimientos y habilidades en el uso de ecuaciones matriciales en este software. No dudes en explorar estos recursos y aprovechar al máximo las herramientas disponibles para mejorar tu comprensión y dominio de las ecuaciones matriciales en Mathematica.

Preguntas frecuentes (FAQ)

1. ¿Qué es una ecuación matricial?

Una ecuación matricial es una expresión que relaciona matrices y vectores, donde se busca encontrar el vector que satisface dicha igualdad.

2. ¿Cuál es la ventaja de utilizar Mathematica para resolver ecuaciones matriciales?

Mathematica ofrece herramientas que facilitan la manipulación de matrices y la resolución de sistemas de ecuaciones, lo que agiliza el proceso y reduce la posibilidad de cometer errores.

3. ¿Cómo se define una matriz en Mathematica?

Para definir una matriz en Mathematica, se utiliza la función "MatrixForm" seguida de los elementos de la matriz separados por comas y encerrados entre llaves.

4. ¿Cuáles son las funciones principales para resolver ecuaciones matriciales en Mathematica?

Las funciones principales son "LinearSolve" y "Inverse". "LinearSolve" se utiliza para resolver sistemas de ecuaciones lineales, mientras que "Inverse" calcula la inversa de una matriz.

5. ¿Cómo se resuelve una ecuación matricial en Mathematica?

Para resolver una ecuación matricial en Mathematica, se utiliza la función "LinearSolve" pasando como argumentos la matriz de coeficientes y el vector de términos independientes.