Aprende a graficar parábolas en Wolfram Mathematica

Cómo identificar el vértice de una parábola dado su ecuación

Para identificar el vértice de una parábola dado su ecuación, debes tener en cuenta la forma de la ecuación general de una parábola, que es y = ax^2 + bx + c. La fórmula para encontrar el vértice de una parábola es V = (-b/2a, f(-b/2a)), donde V representa el punto del vértice, a es el coeficiente cuadrático, b es el coeficiente lineal y c es el término constante.

Por ejemplo, considera la ecuación y = 2x^2 + 4x + 3. Para encontrar el vértice, calculamos x = -4/(22) = -1. Sustituyendo este valor en la ecuación original, obtenemos y = 2(-1)^2 + 4(-1) + 3 = 1. Por lo tanto, el vértice de esta parábola es (-1, 1).

Es importante recordar que cuando a es positivo, la parábola se abre hacia arriba, y cuando a es negativo, la parábola se abre hacia abajo.

Cuál es la diferencia entre una parábola que abre hacia arriba y una que abre hacia abajo

En Wolfram Mathematica, las parábolas pueden abrir hacia arriba o hacia abajo dependiendo del signo del coeficiente principal. Cuando el coeficiente es positivo, la parábola abre hacia arriba, mientras que cuando es negativo, la parábola abre hacia abajo.

Las parábolas que abren hacia arriba tienen un vértice mínimo y una concavidad hacia arriba, mientras que las parábolas que abren hacia abajo tienen un vértice máximo y una concavidad hacia abajo. Esta diferencia en la dirección de apertura tiene un impacto en la forma y la posición de la parábola en el plano cartesiano.

Es importante comprender esta distinción para graficar correctamente las parábolas en Wolfram Mathematica y analizar su comportamiento.

Cómo encontrar los puntos interceptados por una parábola con los ejes x e y

Para encontrar los puntos en los que una parábola intercepta los ejes x e y, debemos recordar que los puntos de intersección con el eje x se encuentran cuando y es igual a cero, mientras que los puntos de intersección con el eje y se encuentran cuando x es igual a cero.

Para los puntos de intersección con el eje x, establecemos y = 0 en la ecuación de la parábola y resolvemos para x. En el caso de una parábola de la forma y = ax^2 + bx + c, podemos igualar y a cero y utilizar la fórmula cuadrática para encontrar las soluciones para x. Estas soluciones son los valores x en los que la parábola cruza el eje x.

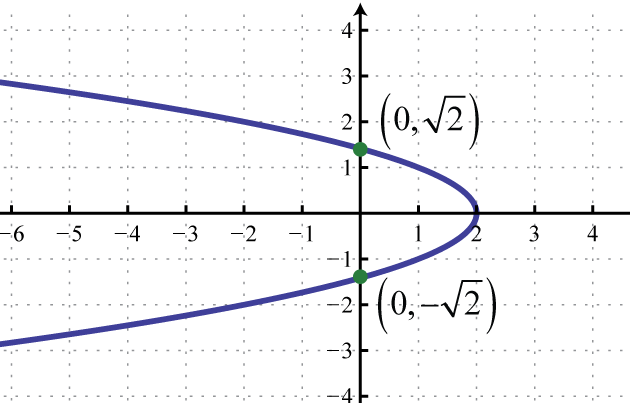
Por otro lado, los puntos de intersección con el eje y se encuentran cuando x es igual a cero. Al establecer x = 0 en la ecuación de la parábola, encontramos el valor de y en el que la parábola cruza el eje y.

Una vez que hayamos encontrado los valores de x y y para los puntos de intersección con los ejes x e y, podemos trazar estos puntos en el plano cartesiano para obtener una representación visual de la parábola.

En Wolfram Mathematica, podemos utilizar la función Solve para resolver la ecuación de la parábola y encontrar los puntos de intersección con los ejes x e y. Esta función nos dará las soluciones en forma de reglas, que podemos convertir en valores numéricos utilizando la función N. Luego, podemos trazar los puntos de intersección utilizando la función Point o Plot.

Para encontrar los puntos interceptados por una parábola con los ejes x e y, establecemos y = 0 y resolvemos para x para los puntos de intersección con el eje x, y establecemos x = 0 y resolvemos para y para los puntos de intersección con el eje y. Utilizando Wolfram Mathematica, podemos resolver la ecuación de la parábola y encontrar estos puntos de intersección de manera eficiente.

Cuál es la ecuación de una parábola cuando se conoce su vértice y un punto en la curva

Para graficar una parábola en Wolfram Mathematica, es importante conocer su ecuación. Si se conoce el vértice (h, k) y un punto (x, y) en la curva, podemos determinar la ecuación utilizando la forma general de una parábola: y = a(x-h)^2 + k.

Sustituyendo las coordenadas del vértice en la ecuación, obtendremos k = a(0-h)^2 + k, lo cual se simplifica a h^2 = 0.

Luego, sustituyendo las coordenadas del punto en la ecuación, obtendremos y = a(x-h)^2 + k, que se simplifica a y = ax^2 - 2ahx + ah^2 + k.

Finalmente, restando la ecuación del vértice de la ecuación del punto, podemos despejar a y encontrar la ecuación de la parábola.

Cuáles son algunas aplicaciones prácticas de las parábolas en el mundo real

Las parábolas son curvas que pueden encontrarse en muchas situaciones en el mundo real. Una de las aplicaciones más comunes es en el campo de la física, donde se utilizan para modelar el movimiento de objetos en caída libre o el comportamiento de proyectiles en vuelo.

Otra aplicación práctica de las parábolas es en el diseño de puentes y arcos. Estas estructuras suelen tener una forma parabólica para distribuir uniformemente las cargas y resistir mejor las fuerzas externas.

En el campo de la óptica, las parábolas también son utilizadas en la fabricación de espejos y lentes. Su forma permite que los rayos de luz se reflejen o refracten de manera precisa para formar imágenes nítidas.

Además, las parábolas se utilizan en la ingeniería de software y en el diseño de algoritmos. Algunos algoritmos de búsqueda y optimización se basan en la forma de una parábola para encontrar soluciones eficientes.

Estos son solo algunos ejemplos de cómo las parábolas tienen aplicaciones prácticas en el mundo real. Aprender a graficarlas en Wolfram Mathematica te permitirá entender mejor su comportamiento y utilizarlas de manera efectiva en diferentes campos.

Cómo graficar una parábola en Wolfram Mathematica

Graficar una parábola en Wolfram Mathematica es una tarea simple pero poderosa. Para comenzar, necesitas entender la ecuación que representa a la parábola. La forma general de la ecuación de una parábola es y = ax^2 + bx + c, donde a, b y c son constantes.

En Wolfram Mathematica, puedes usar la función Plot para graficar una parábola. La sintaxis básica es Plot, donde expr representa la ecuación de la parábola y xmin y xmax delimitan el rango de valores para x.

Por ejemplo, si queremos graficar la parábola y = 2x^2 + 3x - 1, podemos escribir:


Plot


Esto generará un gráfico de la parábola en el rango de x desde -5 hasta 5. Puedes ajustar los valores de a, b y c en la ecuación para ver cómo cambia la forma de la parábola.

Personalizando la gráfica de la parábola

Wolfram Mathematica ofrece muchas opciones para personalizar la apariencia de la gráfica de la parábola. Puedes especificar opciones adicionales dentro de la función Plot para controlar el estilo y los colores. Por ejemplo, puedes usar la opción PlotStyle para cambiar el color de la línea de la gráfica.


Plot


Esto hará que la línea de la gráfica sea de color rojo. Además, puedes agregar etiquetas a los ejes utilizando las opciones AxesLabel y PlotLabel. Estas opciones te permiten proporcionar nombres personalizados para los ejes y el título del gráfico, respectivamente.


Plot


Esto agregará un título al gráfico y etiquetas a los ejes x e y.

Recuerda que puedes experimentar con diferentes valores y opciones para obtener la apariencia deseada de la gráfica de la parábola. Además, puedes combinar varias parábolas en un mismo gráfico utilizando la función Show. Así podrás comparar y analizar múltiples parábolas al mismo tiempo.

Wolfram Mathematica es una poderosa herramienta para graficar parábolas. Con un poco de práctica y experimentación, podrás crear gráficas de parábolas personalizadas y visualmente atractivas. ¡Así que comienza a explorar y descubre todo el potencial que ofrece Wolfram Mathematica!

Cuáles son los pasos para encontrar la ecuación de una parábola a partir de su gráfica en Wolfram Mathematica

En Wolfram Mathematica, graficar una parábola es muy sencillo. Los siguientes pasos te guiarán para encontrar la ecuación de una parábola a partir de su gráfica.

Paso 1: Observa la forma de la parábola

Analiza la curva de la parábola y observa si se abre hacia arriba (concavidad hacia arriba) o hacia abajo (concavidad hacia abajo). Esto te dará una idea de la forma de la ecuación.

Paso 2: Determina la posición de la parábola

Observa la posición de la parábola en el plano cartesiano. El vértice de la parábola te dará información sobre su posición, tanto en el eje x como en el eje y.

Paso 3: Encuentra los puntos adicionales

Identifica al menos dos puntos adicionales en la gráfica de la parábola. Estos puntos te ayudarán a determinar los coeficientes de la ecuación.

Paso 4: Escribe la ecuación de la parábola

Utilizando los datos recopilados de la forma, posición y puntos adicionales, escribe la ecuación de la parábola en su forma general. Asegúrate de incluir los coeficientes adecuados para reflejar la concavidad y la posición de la parábola.

Paso 5: Verifica tu ecuación

Grafica la ecuación que has obtenido en Mathematica y compárala con la gráfica original. Ajusta los coeficientes si es necesario para que la ecuación se ajuste correctamente a la gráfica.

¡Y eso es todo! Siguiendo estos pasos, podrás encontrar la ecuación de cualquier parábola a partir de su gráfica en Wolfram Mathematica. ¡No dudes en practicar con diferentes ejemplos para mejorar tus habilidades de graficación!

Es posible graficar parábolas en 3D utilizando Wolfram Mathematica

Graficar parábolas en 3D puede parecer complicado al principio, pero con Wolfram Mathematica, todo es mucho más sencillo. Esta poderosa herramienta de software permite representar visualmente las ecuaciones de parábolas tridimensionales de forma fácil y precisa.

Para graficar una parábola en 3D en Wolfram Mathematica, primero debemos definir la ecuación de la parábola. Esto se logra ingresando la función correspondiente en el formato adecuado. Por ejemplo, si queremos graficar la parábola y = x^2, simplemente escribimos "Plot3D" en la barra de comandos.