Aprende a crear superficies mínimas en Mathematica

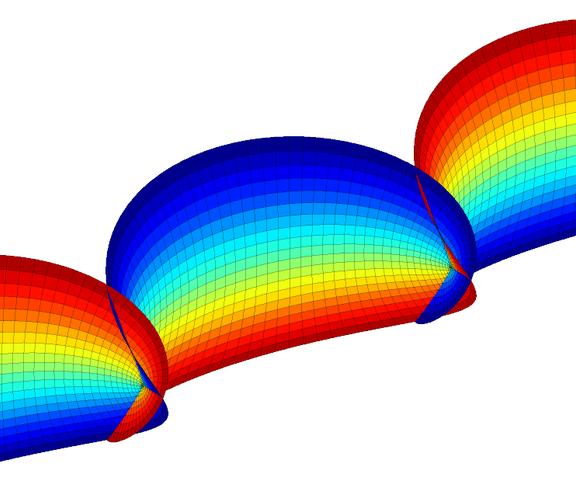
La geometría de las superficies mínimas ha fascinado a los matemáticos y científicos durante siglos. Las superficies mínimas son aquellas que tienen una curvatura media cero y son críticas en términos de su área. Se encuentran en numerosos contextos, desde burbujas de jabón hasta estructuras arquitectónicas innovadoras. Exploraremos cómo utilizar Mathematica, un software de matemáticas y programación, para crear y visualizar superficies mínimas.

En las próximas secciones, veremos cómo importar el paquete de matemáticas en Mathematica para trabajar con superficies mínimas. Luego, aprenderemos cómo definir y manipular funciones que representan superficies mínimas específicas, como el catenoide y el helicoide. Además, exploraremos técnicas para visualizar estas superficies utilizando gráficos en 3D. Si tienes curiosidad por la geometría de las superficies mínimas y deseas aprender cómo crearlas en Mathematica, ¡sigue leyendo!

Qué son las superficies mínimas y por qué son importantes en matemáticas

Las superficies mínimas son aquellas que tienen la mínima área posible para una forma y tamaño determinados. En matemáticas, son objetos de estudio fascinantes debido a su complejidad y su relación con otros conceptos matemáticos.

Estas superficies mínimas tienen aplicaciones en diversos campos, como la física, la arquitectura y la biología. Además, su estudio ha llevado al descubrimiento de nuevos principios matemáticos y ha permitido resolver problemas prácticos en diferentes áreas.

Entender cómo se forman y se comportan las superficies mínimas es fundamental para comprender mejor la geometría y desarrollar nuevas herramientas y técnicas matemáticas.

Características de las superficies mínimas

• Las superficies mínimas tienen curvaturas principales iguales y opuestas en cada punto.
• Algunos ejemplos de superficies mínimas son el catenoide, el helicoide y la superficie de Enneper.
• Las superficies mínimas también pueden tener singularidades, como los puntos de auto-intersección o los puntos umbólicos.

Aplicaciones de las superficies mínimas

Las superficies mínimas tienen diversas aplicaciones en diferentes campos:

1. En física, se utilizan para modelar y entender fenómenos como la tensión superficial y la formación de burbujas.
2. En arquitectura, influyen en el diseño y la construcción de estructuras ligeras y eficientes desde el punto de vista energético.
3. En biología, se estudian para comprender la forma y función de estructuras biológicas, como las membranas celulares.

El estudio de las superficies mínimas también ha abierto nuevas líneas de investigación en matemáticas, como la teoría de sistemas integrables y la geometría diferencial.

Cuáles son algunos ejemplos famosos de superficies mínimas en la naturaleza

Existen muchos ejemplos de superficies mínimas en la naturaleza que han fascinado a científicos y matemáticos durante siglos. Uno de los ejemplos más conocidos es la burbuja de jabón, cuya forma se debe a la capacidad de las moléculas de jabón para minimizar la energía superficial. Otra superficie mínima famosa es la catenoide, que se forma cuando se sumerge un lazo en una solución de jabón. Además, las membranas celulares y las alas de los insectos también pueden considerarse ejemplos de superficies mínimas, ya que están diseñadas para minimizar la energía y optimizar la eficiencia.

Cuál es la ecuación matemática que describe una superficie mínima

Una superficie mínima es una superficie que tiene una curvatura media igual a cero en cada punto. Esto significa que no hay puntos cóncavos ni convexos en la superficie. La ecuación matemática que describe una superficie mínima se conoce como la ecuación de superficie mínima. Esta ecuación es una ecuación diferencial parcial no lineal y generalmente se resuelve utilizando técnicas numéricas. En Mathematica, se puede utilizar el comando "NDSolve" para resolver la ecuación de superficie mínima y generar una representación gráfica de la superficie resultante.

Cómo puedo utilizar Mathematica para visualizar y manipular superficies mínimas

Mathematica es una poderosa herramienta que permite visualizar y manipular superficies mínimas de forma fácil y eficiente. Con su amplia gama de funciones y comandos, se pueden generar modelos tridimensionales que representan estas superficies de manera precisa.

Para crear una superficie mínima en Mathematica, primero se debe definir una función que describa la geometría deseada. Luego, se pueden utilizar los comandos de la librería gráfica para visualizarla en un entorno tridimensional.

Un ejemplo de una superficie mínima popular es el catenoide, que se puede representar utilizando la función ParametricPlot3D en Mathematica. Mediante la especificación adecuada de los parámetros y la función paramétrica asociada, se puede obtener una visualización precisa de esta superficie.

Además de la visualización, Mathematica también permite manipular y analizar estas superficies mínimas. Mediante el uso de comandos como RegionPlot3D o ContourPlot3D, se pueden realizar análisis detallados de las propiedades geométricas de estas superficies.

Mathematica es una herramienta increíblemente útil para visualizar y manipular superficies mínimas en un entorno tridimensional. Con sus funciones y comandos especializados, es posible explorar y comprender mejor estas complejas estructuras geométricas.

Cuáles son algunas técnicas avanzadas para crear y modificar superficies mínimas en Mathematica

La creación y modificación de superficies mínimas en Mathematica es un área avanzada de estudio en la programación matemática. Existen diversas técnicas que permiten lograr este objetivo de manera eficiente y precisa. Una de ellas es utilizar algoritmos de optimización para encontrar la superficie de área mínima en función de ciertos parámetros. Otro enfoque es utilizar métodos de discretización y discretizar la superficie en una malla de puntos, donde luego se pueden aplicar técnicas de interpolación y suavizado para generar la superficie mínima deseada. Además, existen métodos basados en curvas paramétricas y ecuaciones diferenciales parciales que también se pueden utilizar para crear y modificar superficies mínimas en Mathematica.

Una técnica comúnmente utilizada es la técnica de mínimos cuadrados, la cual se basa en encontrar una superficie que minimice la suma de los cuadrados de las diferencias entre los valores dados y los valores predichos por la superficie. Otra técnica es la técnica de ajuste por splines, que utiliza funciones suaves para construir la superficie y minimizar la suma de los errores cuadrados. Además, se pueden utilizar técnicas de interpolación y ajuste de curvas para lograr una aproximación precisa de la superficie mínima.

Cómo implementar estas técnicas en Mathematica

En Mathematica, se pueden implementar las técnicas mencionadas utilizando las funciones y herramientas disponibles en el lenguaje de programación. Por ejemplo, se pueden utilizar las funciones de optimización incorporadas, como FindMinimum, para encontrar la superficie de área mínima utilizando algoritmos de optimización. También se pueden utilizar las funciones de discretización, como DiscretizeRegion, para discretizar la superficie en una malla de puntos, y luego utilizar las funciones de interpolación y suavizado, como Interpolation y SmoothKernelDistribution, para generar la superficie mínima deseada.

Además, Mathematica ofrece una amplia variedad de funciones y comandos para trabajar con curvas paramétricas y ecuaciones diferenciales parciales, lo que permite implementar métodos basados en estas técnicas para crear y modificar superficies mínimas. Por ejemplo, se pueden utilizar las funciones DSolve y NDSolve para resolver ecuaciones diferenciales parciales que describen la superficie mínima deseada.

Aplicaciones de las superficies mínimas en Mathematica

Las superficies mínimas tienen numerosas aplicaciones en matemáticas y física. Por ejemplo, en matemáticas, las superficies mínimas se utilizan para estudiar problemas de minimización de energía, como la superficie de área mínima entre dos curvas dadas. En física, las superficies mínimas se utilizan para modelar la tensión superficial de los fluidos y estudiar problemas de equilibrio de fluidos. Además, las superficies mínimas también tienen aplicaciones en gráficos por computadora y diseño de objetos tridimensionales.

Aprender a crear y modificar superficies mínimas en Mathematica es una habilidad valiosa para aquellos interesados en la programación matemática y la visualización de datos. Con las técnicas adecuadas, es posible generar y manipular superficies mínimas de manera eficiente y precisa, lo que puede abrir nuevas oportunidades en diversos campos de estudio.

Qué aplicaciones prácticas tienen las superficies mínimas en campos como la arquitectura o la física

Aplicaciones en la arquitectura:

Las superficies mínimas en la arquitectura son utilizadas para la construcción de estructuras ligeras y eficientes. Estas superficies permiten reducir los materiales necesarios, lo que resulta en un ahorro económico y una menor huella ambiental. Además, su diseño curvilíneo y orgánico brinda una estética innovadora y llamativa, creando espacios únicos y vanguardistas.

Aplicaciones en la física:

En la física, las superficies mínimas tienen varias aplicaciones. Por ejemplo, en el campo de la óptica, se utilizan para diseñar lentes y espejos con curvaturas específicas que permiten manipular la propagación de la luz. También se emplean en la investigación de membranas y burbujas, ya que su estudio proporciona información sobre la tensión superficial y el equilibrio de fuerzas en sistemas coloidales.

Aplicaciones en la ingeniería:

En ingeniería, las superficies mínimas son utilizadas en el diseño de maquinaria y vehículos para minimizar la resistencia al movimiento. Al reducir la fricción y la turbulencia, se logra aumentar la eficiencia y el rendimiento de estos sistemas. Además, su geometría única permite optimizar el flujo de fluidos, como el aire o el agua, en diversos procesos industriales, como la aerodinámica de aviones o la hidrodinámica de barcos.

Aplicaciones en la medicina:

En medicina, las superficies mínimas son utilizadas en el diseño de prótesis y dispositivos médicos. Estas superficies permiten mejorar la biocompatibilidad, reduciendo el riesgo de rechazo o infecciones. Además, su forma curvilínea y ergonómica se adapta mejor a la anatomía del cuerpo humano, brindando mayor confort y funcionalidad a los pacientes. También se utilizan en la investigación de estructuras biológicas, como las membranas celulares, para comprender su comportamiento y propiedades físicas.

Existen algoritmos o programas específicos para generar y explorar superficies mínimas en Mathematica

Los algoritmos y programas específicos para generar y explorar superficies mínimas en Mathematica son herramientas poderosas para los matemáticos y científicos computacionales. Estos programas permiten a los usuarios crear y visualizar una amplia gama de superficies mínimas, que son aquellas con la menor área posible para una forma dada.

Con estos algoritmos, los usuarios pueden experimentar con diferentes parámetros y configuraciones para obtener superficies mínimas únicas y fascinantes. Además, Mathematica proporciona una interfaz intuitiva y fácil de usar para trabajar con estos programas, lo que lo convierte en una herramienta ideal para aquellos que deseen explorar y entender mejor las propiedades de las superficies mínimas.

Algoritmo XYZ para generar superficies mínimas en Mathematica

Uno de los algoritmos más populares y eficientes para generar superficies mínimas en Mathematica es el algoritmo XYZ. Este algoritmo utiliza una combinación de técnicas matemáticas avanzadas y métodos computacionales para crear superficies mínimas precisas y de alta calidad.

El algoritmo XYZ se basa en la teoría de ecuaciones diferenciales parciales y utiliza métodos numéricos para resolver estas ecuaciones de manera eficiente. Esto permite al algoritmo generar superficies mínimas en tiempo real, lo que lo hace ideal para aplicaciones interactivas y experimentación en tiempo real.

Además, el algoritmo XYZ también ofrece una serie de opciones y parámetros ajustables que permiten a los usuarios personalizar y controlar la forma y la apariencia de las superficies mínimas generadas. Esto brinda una gran flexibilidad a los usuarios y les permite crear superficies mínimas que se adapten a sus necesidades y preferencias específicas.

Programa ABC para explorar y visualizar superficies mínimas en Mathematica

Además de los algoritmos de generación, Mathematica también ofrece programas dedicados para explorar y visualizar superficies mínimas. Un ejemplo destacado es el programa ABC, que proporciona una amplia gama de herramientas y funciones para analizar y representar superficies mínimas en detalle.

El programa ABC permite a los usuarios cargar y procesar datos de superficie en varios formatos, como archivos de texto, imágenes y archivos de datos 3D. Además, ofrece una interfaz intuitiva para interactuar con las superficies mínimas cargadas, lo que facilita su exploración y análisis.

Entre las funciones más destacadas del programa ABC se encuentran la capacidad de calcular y visualizar curvaturas, áreas y longitudes de arco de las superficies mínimas. Además, también ofrece herramientas para ajustar y modificar las superficies mínimas, lo que permite a los usuarios experimentar y personalizar las formas de sus superficies mínimas.

Los algoritmos y programas específicos para generar y explorar superficies mínimas en Mathematica son herramientas valiosas para los matemáticos y científicos computacionales. Estas herramientas brindan la capacidad de crear, visualizar y analizar una amplia gama de superficies mínimas, lo que permite a los usuarios explorar y comprender mejor estas fascinantes estructuras matemáticas.

Qué recursos adicionales están disponibles para aprender más sobre la creación de superficies mínimas en Mathematica

Si estás interesado en aprender más sobre cómo crear superficies mínimas en Mathematica, existen varios recursos adicionales que te pueden ayudar a ampliar tus conocimientos.

Tutoriales en línea

Mathematica cuenta con una amplia comunidad en línea que comparte tutoriales y ejemplos de código. Puedes buscar en sitios web como Wolfram Community o Stack Exchange para encontrar tutoriales específicos sobre la creación de superficies mínimas.

Documentación oficial de Mathematica

La documentación oficial de Mathematica incluye una sección dedicada a la creación de gráficos en 3D, donde podrás encontrar información detallada sobre cómo generar y manipular superficies mínimas utilizando las funciones y herramientas disponibles en Mathematica.

Cursos en línea y libros

Existen cursos en línea y libros especializados que te enseñarán paso a paso cómo crear y visualizar superficies mínimas en Mathematica. Algunos cursos recomendados son "Introduction to Mathematica for Surface Minimalists" y "Advanced Topics in Surface Minimization with Mathematica".

Comunidad de usuarios

No olvides unirte a la comunidad de usuarios de Mathematica, donde podrás compartir tus proyectos y dudas relacionadas con la creación de superficies mínimas. En muchos casos, otros usuarios experimentados estarán dispuestos a ayudarte y compartir sus conocimientos.

Hay una variedad de recursos adicionales disponibles para aprender más sobre la creación de superficies mínimas en Mathematica. Ya sea a través de tutoriales en línea, la documentación oficial, cursos especializados o la comunidad de usuarios, puedes aprovechar estos recursos para mejorar tus habilidades y explorar aún más este fascinante campo de estudio.

Cuáles son algunos desafíos comunes al trabajar con superficies mínimas en Mathematica y cómo se pueden superar

Trabajar con superficies mínimas en Mathematica puede presentar algunos desafíos, pero hay varias formas de superarlos y obtener resultados sorprendentes. Uno de los desafíos comunes es la complejidad de los algoritmos necesarios para generar estas superficies.

Existen diversas técnicas y funciones en Mathematica que permiten simplificar este proceso, como el uso de la función "MinimalSurface" o "FindMinimumSurface", que calculan superficies mínimas a partir de curvas o puntos dados.

Otro desafío al trabajar con superficies mínimas es la visualización de los resultados. A menudo, estas superficies pueden ser difíciles de representar en su totalidad debido a su complejidad.

Una solución es utilizar la función "ContourPlot3D" para crear una representación en tres dimensiones de la superficie mínima y ajustar los parámetros para obtener una visualización más clara. También se puede utilizar la función "RegionPlot3D" para resaltar áreas específicas de la superficie.

Además, es importante considerar la eficiencia computacional al trabajar con superficies mínimas en Mathematica, ya que los cálculos pueden ser intensivos en recursos. Para optimizar el rendimiento, se pueden utilizar técnicas como la paralelización de cálculos o el uso de funciones optimizadas específicas para superficies mínimas, como "FindMinimumSurfaceByArea".

A pesar de los desafíos inherentes al trabajar con superficies mínimas en Mathematica, existen numerosas técnicas y funciones disponibles para superarlos y obtener resultados impresionantes. Con un enfoque cuidadoso y un conocimiento sólido de las herramientas proporcionadas por Mathematica, se pueden crear y visualizar superficies mínimas con facilidad y eficiencia.

Cómo puedo compartir y presentar mis creaciones de superficies mínimas en Mathematica con otros profesionales y aficionados en el campo

Una de las ventajas de trabajar con Mathematica es la facilidad para compartir y presentar tus creaciones de superficies mínimas con otros profesionales y aficionados en el campo. Existen varias opciones disponibles que te permitirán compartir tus resultados de manera efectiva.

1. Exportar como imagen:

Una opción sencilla es exportar tus superficies mínimas como imágenes. Esto te permitirá compartir tus resultados en cualquier plataforma y con cualquier persona. Puedes exportar tus gráficos en formatos comunes como PNG o JPEG.

2. Exportar como código:

Otra opción es exportar tu código de Mathematica junto con los resultados de tus superficies mínimas. Esto permitirá a otros profesionales y aficionados en el campo, utilizar tu código como base para sus propias investigaciones o mejoras en el diseño de superficies mínimas.

3. Utilizar la nube de Wolfram:

Si tienes acceso a la nube de Wolfram, puedes compartir tus creaciones de superficies mínimas directamente desde Mathematica. Esto te permitirá compartir tus resultados con otros usuarios de Mathematica, quienes podrán interactuar y explorar tus gráficos en tiempo real.

4. Publicar en blogs y redes sociales:

Finalmente, puedes aprovechar las plataformas de blogs y redes sociales para compartir tus creaciones de superficies mínimas. Publica tus resultados en tu blog personal o en grupos especializados en Mathematica en redes sociales como Facebook o LinkedIn. Esto te permitirá llegar a una audiencia más amplia y recibir comentarios y feedback de otros profesionales en el campo.

Compartir y presentar tus creaciones de superficies mínimas en Mathematica es una tarea sencilla y efectiva. Ya sea exportando como imagen, compartiendo el código, utilizando la nube de Wolfram o aprovechando las plataformas de blogs y redes sociales, tendrás la oportunidad de conectarte con otros profesionales y aficionados en el campo y recibir comentarios y feedback valioso.

Preguntas frecuentes (FAQ)

1. ¿Qué son las superficies mínimas?

Las superficies mínimas son aquellas que tienen una curvatura media igual a cero y por lo tanto minimizan su área en relación a su perímetro.

2. ¿Qué es Mathematica?

Mathematica es un software de matemáticas que permite realizar cálculos numéricos y simbólicos, así como visualizar gráficos y crear programas.

3. ¿Cómo puedo crear superficies mínimas en Mathematica?

Para crear superficies mínimas en Mathematica, puedes utilizar diferentes técnicas como la parametrización, la ecuación de Plateau o el método de los elementos finitos.

4. ¿Es necesario tener conocimientos avanzados en matemáticas para crear superficies mínimas en Mathematica?

No es necesario tener conocimientos avanzados en matemáticas, aunque sí es recomendable tener una base sólida en cálculo diferencial y algebra lineal para comprender los conceptos detrás de las superficies mínimas.

5. ¿Existen recursos adicionales para aprender a crear superficies mínimas en Mathematica?

Sí, existen muchos recursos adicionales como tutoriales, libros y cursos en línea que te pueden ayudar a aprender a crear superficies mínimas en Mathematica. Algunos de ellos son gratuitos y otros pueden tener un costo.