Aprende a crear animaciones en Mathematica para sistemas físicos

Mathematica es una poderosa herramienta computacional utilizada en diversas áreas, desde la física hasta la economía. Una de las características más interesantes de Mathematica es su capacidad para crear animaciones que permiten visualizar y comprender mejor fenómenos físicos y matemáticos. Exploraremos cómo utilizar Mathematica para crear animaciones de sistemas físicos, lo cual es especialmente útil tanto para el aprendizaje como para la investigación en esta área.

En las siguientes secciones, aprenderemos los conceptos básicos de la creación de animaciones en Mathematica, incluyendo cómo definir variables, funciones y ecuaciones diferenciales que describen el sistema físico que queremos animar. También veremos cómo utilizar la función "Animate" de Mathematica para generar la animación correspondiente, ajustando parámetros como el tiempo de duración, la velocidad de reproducción y las opciones de visualización. Asimismo, exploraremos algunas técnicas avanzadas para mejorar nuestras animaciones y mostrar resultados más realistas y de mayor precisión. Si estás interesado en la física y quieres dar vida a tus sistemas físicos, sigue leyendo para descubrir cómo crear animaciones impresionantes con Mathematica.

Cuáles son las herramientas básicas para crear animaciones en Mathematica

Para crear animaciones en Mathematica, es necesario tener conocimientos básicos de programación en este lenguaje. Algunas de las herramientas básicas que se utilizan son:

1. Función Animate

La función Animate es la herramienta principal para crear animaciones en Mathematica. Permite cambiar los parámetros de una expresión o función en un rango determinado, generando una secuencia de imágenes que se visualizan como una animación.

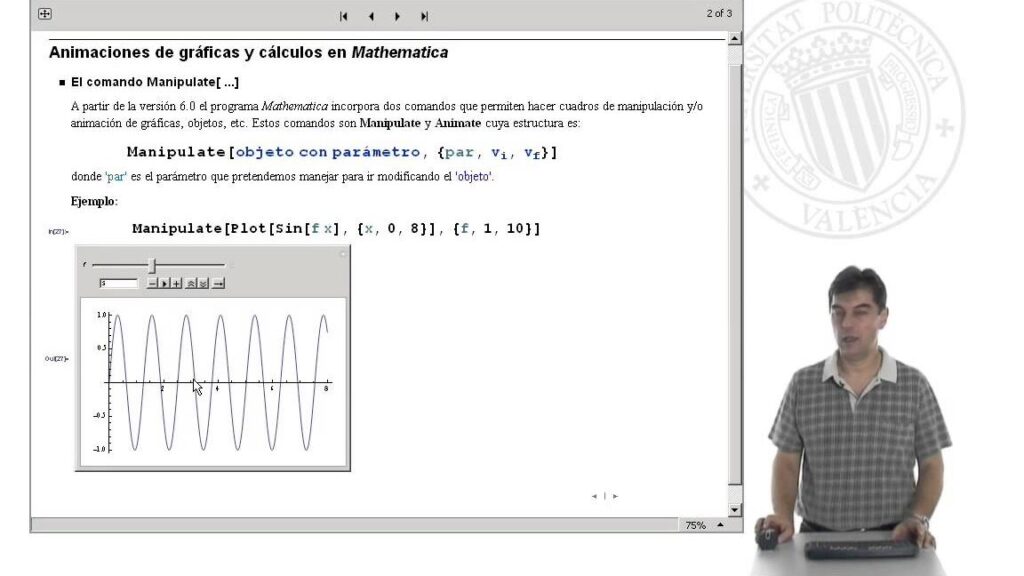
2. Manipulate

Manipulate es otra función útil en Mathematica para crear animaciones interactivas. Permite controlar los parámetros de una expresión o función en tiempo real, lo que facilita la experimentación y la visualización de cambios.

3. Gráficos y visualización

Para crear animaciones visuales en Mathematica, se utilizan las funciones gráficas y de visualización incluidas en el lenguaje. Estas herramientas permiten crear gráficos 2D y 3D, manipular objetos y cambiar su posición, tamaño y apariencia.

4. Tiempo y velocidad

Para controlar el tiempo y la velocidad de la animación, se utilizan las funciones relacionadas con el tiempo en Mathematica. Estas funciones permiten especificar la duración de la animación y regular la velocidad de reproducción de las imágenes.

5. Exportación de animaciones

Una vez creada la animación, es posible exportarla a diferentes formatos, como GIF, video o secuencia de imágenes. Mathematica ofrece diversas opciones para exportar las animaciones y ajustar sus características, como la resolución y la calidad.

Con estas herramientas básicas, es posible crear animaciones en Mathematica para representar y visualizar sistemas físicos de manera dinámica y interactiva.

Cómo se define un sistema físico en Mathematica

En Mathematica, un sistema físico se define mediante la creación de ecuaciones diferenciales que describen su comportamiento. Estas ecuaciones pueden ser escritas en forma simbólica o numérica, dependiendo de las necesidades del sistema en cuestión.

Para definir un sistema físico en Mathematica, primero se deben establecer las variables y constantes involucradas. Luego, se definen las ecuaciones que relacionan estas variables en función del tiempo.

Una vez definido el sistema físico, Mathematica proporciona herramientas para simular y visualizar su comportamiento a lo largo del tiempo. Esto permite estudiar y analizar el sistema, así como crear animaciones que ilustren su evolución en el espacio y tiempo.

Ejemplo de creación de una animación en Mathematica

Supongamos que queremos simular el movimiento de un péndulo simple. Para ello, necesitamos definir las ecuaciones diferenciales que describen su comportamiento.

En primer lugar, establecemos las variables involucradas, que en este caso son el ángulo del péndulo (theta) y su velocidad angular (omega). También establecemos la longitud del péndulo (L) y la aceleración debido a la gravedad (g).

A continuación, definimos las ecuaciones que relacionan estas variables en función del tiempo. En el caso del péndulo simple, estas ecuaciones son:

theta'' + (g/L) Sin] == 0
omega == D, t]

Una vez definidas las ecuaciones, podemos utilizar las funciones de simulación y visualización de Mathematica para generar la animación del péndulo en movimiento.

Por ejemplo, podemos utilizar la función "Animate" de Mathematica para crear una animación que muestre el movimiento del péndulo a lo largo del tiempo. Esta función permite controlar diversos parámetros de la animación, como la velocidad de reproducción y el rango de tiempo.

Con Mathematica es posible definir sistemas físicos y crear animaciones que ilustren su comportamiento. Esto permite visualizar y comprender mejor fenómenos físicos complejos, como el movimiento de un péndulo o el comportamiento de un sistema dinámico.

Es importante destacar que Mathematica es una poderosa herramienta para realizar cálculos simbólicos y numéricos, lo que facilita el estudio y análisis de sistemas físicos en diversos campos de la ciencia y la ingeniería.

Qué tipos de animaciones se pueden crear utilizando Mathematica

Mathematica es una poderosa herramienta que permite crear una amplia gama de animaciones para representar sistemas físicos. Al utilizar esta herramienta, los usuarios pueden crear animaciones 2D y 3D que representen el comportamiento de fenómenos físicos complejos. Algunos ejemplos populares de animaciones que se pueden crear en Mathematica incluyen la representación del movimiento de partículas, la dinámica de fluidos, la oscilación de sistemas mecánicos y la propagación de ondas. La flexibilidad de Mathematica permite a los usuarios personalizar sus animaciones, ajustando parámetros como la escala de tiempo y los colores utilizados.

Una ventaja clave de utilizar Mathematica para crear animaciones es que los usuarios pueden combinar código y gráficos interactivos para mejorar la visualización de fenómenos físicos. Esto significa que los usuarios pueden agregar controles deslizantes, botones y otros elementos interactivos a sus animaciones, lo que permite a los espectadores explorar diferentes escenarios y ajustar parámetros en tiempo real. Esta funcionalidad interactiva brinda una experiencia más inmersiva y educativa, ya que los espectadores pueden experimentar directamente cómo cambia el comportamiento del sistema físico en respuesta a diferentes variables.

Cómo crear animaciones en Mathematica

Para crear animaciones en Mathematica, los usuarios deben utilizar la función "Animate" o la función "Manipulate" en combinación con gráficos y código que describan el sistema físico que desean animar. Con la función "Animate", los usuarios pueden especificar los parámetros iniciales del sistema y definir cómo cambian esos parámetros con el tiempo. Con la función "Manipulate", los usuarios pueden agregar controles interactivos para ajustar los parámetros en tiempo real.

Una vez que los usuarios han definido los parámetros y las funciones necesarias, pueden usar las herramientas gráficas de Mathematica para representar el sistema físico. Por ejemplo, pueden utilizar funciones de gráficos como "Plot", "ParametricPlot" o "VectorPlot" para visualizar la evolución en el tiempo de una variable, una ecuación diferencial o un campo vectorial, respectivamente. Luego, pueden combinar estas representaciones gráficas con la función "Animate" o "Manipulate" para crear la animación.

Además de las funciones gráficas básicas, Mathematica también ofrece una amplia gama de opciones de estilo y diseño para personalizar la apariencia de las animaciones. Los usuarios pueden ajustar los colores, la opacidad, los grosores de línea y muchos otros atributos visuales de sus gráficos.

Mathematica ofrece a los usuarios una poderosa herramienta para crear animaciones de sistemas físicos. Esta herramienta combina la flexibilidad de programación con la capacidad de visualización interactiva, lo que permite a los usuarios representar y explorar fenómenos físicos complejos de manera eficiente y efectiva.

Cuáles son los principios fundamentales de la animación en sistemas físicos

La animación en sistemas físicos es una herramienta poderosa para visualizar conceptos abstractos y complejos. Los principios fundamentales de la animación en sistemas físicos giran en torno a la representación gráfica de fenómenos físicos, utilizando elementos visuales y movimientos para comunicar de manera efectiva ideas y conceptos.

En primer lugar, es crucial comprender los conceptos básicos de la física que se desea animar. Esto incluye comprender las leyes fundamentales, como la conservación de la energía y el momento, así como las interacciones entre diferentes objetos y fuerzas.

Además, es importante tener en cuenta los aspectos técnicos de la animación. Esto implica utilizar un software adecuado, como Mathematica, que ofrece herramientas y funciones específicas para la creación de animaciones en sistemas físicos. También implica comprender los conceptos básicos de la programación, como el manejo de variables y cálculos matemáticos.

Otro principio fundamental es la precisión en la representación de los sistemas físicos. Esto implica tener en cuenta las dimensiones y escalas adecuadas, así como la precisión numérica en los cálculos utilizados. Una representación precisa asegura que las animaciones sean realistas y se ajusten a los principios físicos subyacentes.

Finalmente, es importante tener en cuenta la estética visual en la animación. Esto implica utilizar colores, formas y tamaños adecuados para resaltar aspectos importantes de los sistemas físicos. También implica utilizar movimientos suaves y fluidos para representar de manera efectiva los fenómenos físicos en acción.

Cuáles son los pasos para crear una animación en Mathematica

Crear animaciones en Mathematica puede parecer intimidante al principio, pero siguiendo unos simples pasos podrás lograr resultados sorprendentes. Primero, necesitarás tener instalado Mathematica en tu computadora. Luego, debes familiarizarte con el lenguaje de programación Wolfram, que es utilizado por Mathematica. Una vez que tengas estos dos requisitos, estás listo para empezar a crear tus animaciones.

El primer paso es definir las ecuaciones que describen el sistema físico que deseas animar. Puedes utilizar las funciones y operadores matemáticos de Mathematica para esto. Luego, debes crear una lista de valores para los parámetros de las ecuaciones. Estos valores representarán los diferentes estados del sistema a lo largo del tiempo. Con estos dos elementos en su lugar, puedes proceder a crear la animación.

Creando la animación paso a paso

El segundo paso es configurar los parámetros de la animación. Puedes elegir la duración de la animación, la velocidad de reproducción y otras opciones personalizadas. Una vez que hayas configurado estos parámetros, es momento de generar los gráficos estáticos para cada uno de los valores de los parámetros. Puedes utilizar las funciones de graficación de Mathematica para esto.

Una vez que hayas generado los gráficos estáticos, llega el momento de crear la animación propiamente dicha. Para esto, puedes utilizar la función "ListAnimate" de Mathematica, que toma como argumento la lista de gráficos estáticos que has generado previamente. También puedes personalizar la apariencia de la animación, como los colores, estilos y escalas.

Finalmente, una vez que hayas creado la animación, puedes guardarla en diferentes formatos, como GIF o video. También puedes exportarla como código HTML para mostrarla en una página web. La creación de animaciones en Mathematica puede ser un proceso creativo y desafiante, pero los resultados valen la pena.

Cuál es la sintaxis básica para animar objetos en Mathematica

En Mathematica, la animación de objetos se realiza utilizando la función Animate. La sintaxis básica es la siguiente:

Animate

Donde expr es la expresión que describe el objeto que quieres animar, t es el parámetro de tiempo, tmin y tmax son los valores mínimo y máximo de t, y dt es el intervalo de tiempo entre cada frame de la animación.

Por ejemplo, si quisieras animar un objeto que se mueve a lo largo de una línea recta en el intervalo de tiempo de 0 a 10, con un intervalo de tiempo de 0.1, usarías la siguiente sintaxis:

Animate], {t, 0, 10, 0.1}]

Esta sintaxis básica puede ser modificada y adaptada para crear animaciones más complejas en Mathematica.

Cómo se pueden agregar efectos especiales a las animaciones en Mathematica

En Mathematica, se pueden agregar efectos especiales a las animaciones para hacerlas más atractivas y realistas. Una forma de lograrlo es utilizando la función Animate. Con Animate, puedes especificar una variable de control y una serie de valores a través de los cuales la animación debe transitar. Esto te permite crear animaciones en las que los objetos se mueven, cambian de forma o incluso interactúan entre sí.

Otro método para agregar efectos especiales a tus animaciones es utilizando la función Manipulate. Con Manipulate, puedes crear controles deslizantes, botones y otros elementos interactivos que te permiten ajustar diferentes parámetros de la animación en tiempo real. Esto te da un mayor control sobre cómo se ve y se comporta la animación.

También puedes utilizar técnicas avanzadas como la iluminación, la sombra y los efectos de partículas para agregar aún más realismo a tus animaciones en Mathematica. Estos efectos se pueden lograr utilizando las funciones Lighting, Shadow, ParticleSystems, entre otras.

Cuáles son las ventajas de utilizar Mathematica para crear animaciones en sistemas físicos

Utilizar Mathematica para crear animaciones en sistemas físicos presenta numerosas ventajas. En primer lugar, Mathematica es una potente herramienta de programación que permite una representación matemática precisa de los fenómenos físicos. Esto facilita la creación de animaciones realistas y precisas.

Otra ventaja de utilizar Mathematica es su amplia librería de funciones y algoritmos. Esto permite ahorrar tiempo y esfuerzo al no tener que programar cada detalle desde cero. Además, Mathematica también ofrece una interfaz gráfica intuitiva que simplifica el proceso de creación de animaciones.

Además, Mathematica cuenta con herramientas de simulación que permiten modelar y visualizar sistemas físicos complejos. Esto es especialmente útil para comprender fenómenos difíciles de imaginar o visualizar en la realidad.

Por último, Mathematica ofrece la posibilidad de exportar las animaciones en diversos formatos, lo que facilita compartir y presentar los resultados de manera efectiva.

Existen recursos en línea para aprender más sobre la creación de animaciones en Mathematica

La creación de animaciones en Mathematica puede ser una poderosa herramienta para visualizar sistemas físicos en acción. Si estás interesado en aprender más sobre cómo crear animaciones en Mathematica, hay varios recursos en línea disponibles para ayudarte a comenzar.

Una excelente opción es el sitio web oficial de Wolfram, donde puedes encontrar documentación detallada y ejemplos de código para crear animaciones utilizando las funciones y capacidades de animación incorporadas en Mathematica.

Otro recurso útil es el canal de YouTube de Wolfram, que ofrece una variedad de tutoriales en video sobre cómo crear animaciones en Mathematica. Estos videos son una excelente manera de aprender visualmente y seguir paso a paso a medida que creas tus propias animaciones.

Además, hay varios blogs y foros en línea dedicados a Mathematica, donde puedes encontrar consejos, trucos y ejemplos de animaciones creadas por la comunidad de usuarios de Mathematica. Estos recursos son excelentes para obtener inspiración y aprender de las experiencias de otros.

No olvides que la práctica es clave para mejorar tu habilidad para crear animaciones en Mathematica. ¡No temas experimentar y probar diferentes enfoques y configuraciones para obtener los resultados deseados!

Hay ejemplos de animaciones en sistemas físicos creadas con Mathematica disponibles para su estudio y análisis

Si estás interesado en aprender cómo crear animaciones en Mathematica para sistemas físicos, estás en el lugar correcto. En este artículo, te mostraré ejemplos de animaciones que puedes utilizar como punto de partida para tus propios proyectos.

Con Mathematica, puedes generar animaciones realistas y dinámicas que ayudarán a visualizar conceptos físicos complicados. Ya sea que estés estudiando mecánica clásica, termodinámica o electromagnetismo, las animaciones pueden ser una herramienta invaluable para comprender mejor los principios subyacentes.

Una de las ventajas de usar Mathematica para crear animaciones en sistemas físicos es la facilidad con la que puedes manipular los parámetros de tu simulación. Puedes ajustar la velocidad, el tamaño, las condiciones iniciales y otras variables para ver cómo cambia el comportamiento del sistema en tiempo real.

Además, Mathematica te permite exportar tus animaciones en diferentes formatos, como GIF, AVI o HTML5, para que puedas compartir tus resultados con otros y crear contenido interactivo. Esto es especialmente útil si estás enseñando o divulgando conceptos físicos.

En los siguientes apartados, exploraremos algunos ejemplos de animaciones en sistemas físicos creadas con Mathematica. Cada ejemplo estará acompañado de su correspondiente código, para que puedas entender cómo se creó y personalizarlo según tus necesidades.

Simulación de caída libre

Uno de los conceptos más básicos en la física es la caída libre. Cuando un objeto cae en ausencia de fuerzas de resistencia, su movimiento sigue una trayectoria parabólica. Con Mathematica, puedes simular este fenómeno y visualizarlo en tiempo real.


Animate(
Graphics({
Red, PointSize(0.02), Point({0, -9.8 t^2/2})
}),
{t, 0, 5}
)


En este ejemplo, el objeto se representa como un punto rojo que se desplaza hacia abajo a medida que pasa el tiempo. La ecuación que describe su posición en función del tiempo es -9.8 t^2/2, donde t es el tiempo en segundos.

Usando la función Animate, podemos crear una animación que muestra cómo el punto se mueve a medida que t varía de 0 a 5 segundos. Puedes ajustar los límites de tiempo según tus necesidades.

Simulación de órbitas planetarias

Otro aspecto fascinante de la física es el estudio de las órbitas planetarias. Utilizando las leyes de Kepler y las ecuaciones de movimiento de Newton, Mathematica puede generar animaciones que representan el movimiento de los planetas alrededor del sol.


Animate(
Graphics({
Yellow, PointSize(0.05), Point({Cos, Sin})
}),
{t, 0, 2 Pi}
)


En este ejemplo, el objeto amarillo representa un planeta que se mueve en una trayectoria circular alrededor del origen (que representa el sol). La ecuación que describe su posición en función del tiempo es (Cos, Sin), donde t es el ángulo en radianes.

Usando la función Animate, podemos crear una animación que muestra cómo el planeta se desplaza a medida que t varía de 0 a 2π (un ciclo completo). Puedes ajustar los límites de tiempo según tus necesidades.

En este artículo, exploramos cómo crear animaciones en Mathematica para sistemas físicos. Las animaciones pueden ser una poderosa herramienta para visualizar conceptos complicados y comprender mejor los principios fundamentales de la física.

Con Mathematica, puedes generar animaciones realistas y dinámicas que te permiten manipular los parámetros de tu simulación y ver los efectos en tiempo real. Además, puedes exportar tus animaciones en diferentes formatos para compartir tus resultados y crear contenido interactivo.

Espero que estos ejemplos te hayan inspirado a experimentar y crear tus propias animaciones en sistemas físicos con Mathematica. ¡Diviértete explorando las posibilidades y descubriendo nuevos fenómenos!

Preguntas frecuentes (FAQ)

1. ¿Necesito conocimientos previos en Mathematica para poder crear animaciones?

No, este tutorial está diseñado para principiantes y no requiere conocimientos previos en Mathematica. Te guiará paso a paso en el proceso de creación de animaciones.

2. ¿Qué tipo de sistemas físicos puedo simular con las animaciones en Mathematica?

Puedes simular una amplia variedad de sistemas físicos, como movimientos de partículas, oscilaciones, colisiones, trayectorias de proyectiles, entre otros.

3. ¿Puedo personalizar las animaciones según mis necesidades?

Sí, Mathematica te permite personalizar las animaciones de acuerdo a tus necesidades. Puedes ajustar los parámetros, cambiar los colores, agregar etiquetas, entre otras opciones de personalización.

4. ¿Puedo exportar las animaciones a otros formatos para compartir con otros?

Sí, Mathematica te permite exportar las animaciones en diferentes formatos, como GIF, AVI, MP4, entre otros. De esta manera, podrás compartir tus animaciones con otros y utilizarlas en presentaciones o publicaciones.

5. ¿Puedo utilizar las animaciones en mis proyectos académicos o profesionales?

¡Claro! Las animaciones creadas en Mathematica son una excelente herramienta para enriquecer tus proyectos académicos o profesionales. Puedes utilizarlas para visualizar y comunicar conceptos complejos de forma más clara y efectiva.