Aprende a calcular el coseno y seno hiperbólico en Mathematica

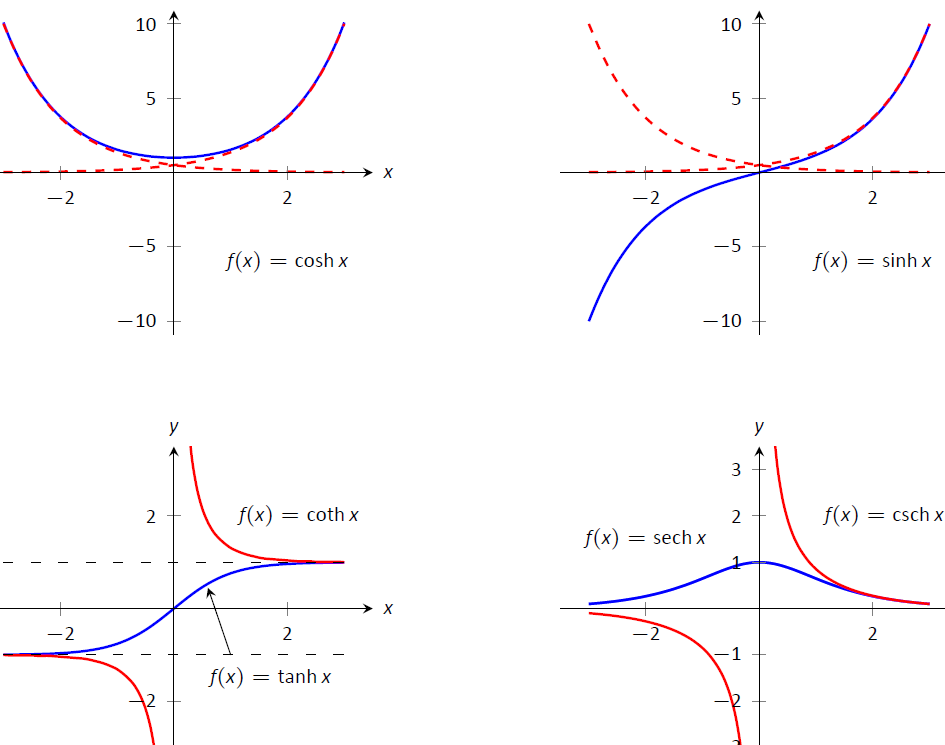
En el campo de las matemáticas y la programación, el coseno y seno hiperbólico son dos funciones importantes que se utilizan para modelar fenómenos físicos y cálculos matemáticos avanzados. Estas funciones son similares a las funciones trigonométricas tradicionales, pero están basadas en la función exponencial.

Aprenderemos cómo calcular el coseno y seno hiperbólico utilizando el software Mathematica. Explicaremos los conceptos básicos de estas funciones y proporcionaremos ejemplos prácticos para que puedas implementarlos en tus propios proyectos o investigaciones matemáticas. Además, te mostraremos cómo utilizar las herramientas de visualización de Mathematica para representar gráficamente los resultados obtenidos. ¡Prepárate para sumergirte en el fascinante mundo del coseno y seno hiperbólico con Mathematica!

Cuál es la fórmula para calcular el coseno hiperbólico en Mathematica

Para calcular el coseno hiperbólico en Mathematica, puedes utilizar la función "Cosh". Esta función devuelve el coseno hiperbólico de un número dado. La sintaxis para calcular el coseno hiperbólico de un número "x" es la siguiente:

Cosh

Por ejemplo, si queremos calcular el coseno hiperbólico de 2, podemos escribir:

Cosh

El resultado será aproximadamente 3.762195...

Es importante tener en cuenta que Mathematica utiliza radianes como unidad para los argumentos trigonométricos. Así que asegúrate de convertir los ángulos a radianes si es necesario.

Usando la función "Sinh" para calcular el seno hiperbólico

Además del coseno hiperbólico, Mathematica también ofrece la función "Sinh" para calcular el seno hiperbólico. Esta función devuelve el seno hiperbólico de un número dado.

La sintaxis para calcular el seno hiperbólico de un número "x" es la siguiente:

Sinh

Por ejemplo, si queremos calcular el seno hiperbólico de 2, podemos escribir:

Sinh

El resultado será aproximadamente 3.62686...

Al igual que con la función "Cosh", asegúrate de convertir los ángulos a radianes si es necesario al utilizar la función "Sinh".

Cuál es la fórmula para calcular el seno hiperbólico en Mathematica

El seno hiperbólico es una función matemática que se utiliza para calcular valores trigonométricos en el contexto de las funciones hiperbólicas. En Mathematica, puedes calcular el seno hiperbólico utilizando la función "Sinh". La fórmula general para calcular el seno hiperbólico es:

sinh(x) = (e^x - e^(-x))/2

Donde "x" es el valor de entrada para el cálculo.

En Mathematica, simplemente puedes usar la función "Sinh" seguida del valor de entrada entre paréntesis para calcular el seno hiperbólico. Por ejemplo:

Sinh(x)

Esto te dará el resultado del cálculo del seno hiperbólico para el valor de "x" que ingreses. Recuerda que la función "Sinh" está diseñada para trabajar con valores numéricos y no con variables simbólicas.

Si quieres calcular el seno hiperbólico de un ángulo en radianes, primero debes convertir el ángulo a radianes utilizando la función "Degree". Por ejemplo:

Sinh(Degree(x))

Esto te dará el resultado del cálculo del seno hiperbólico para el ángulo convertido a radianes.

Cómo puedo utilizar la función "Cosh" para calcular el coseno hiperbólico en Mathematica

En Mathematica, podemos utilizar la función "Cosh" para calcular el coseno hiperbólico de un número. La sintaxis para utilizar esta función es la siguiente: Cosh, donde x es el número al cual queremos calcular su coseno hiperbólico.

Por ejemplo, si queremos calcular el coseno hiperbólico de 2, simplemente escribimos Cosh y Mathematica nos dará como resultado el valor aproximado de 3.7622.

Es importante tener en cuenta que el coseno hiperbólico se define como la relación entre la exponencial de un número y la exponencial de su opuesto. Por lo tanto, el coseno hiperbólico de x se puede expresar como (e^x + e^-x)/2.

Es posible calcular el coseno hiperbólico de números complejos utilizando la función "Cosh". Por ejemplo, si queremos calcular el coseno hiperbólico de i, donde i es la unidad imaginaria, simplemente escribimos Cosh y Mathematica nos dará como resultado el valor aproximado de 0.540302 + 0.841471i.

Cómo puedo utilizar la función "Sinh" para calcular el seno hiperbólico en Mathematica

En Mathematica, puedes usar la función "Sinh" para calcular el seno hiperbólico de un número. La función "Sinh" devuelve el valor del seno hiperbólico de un número específico. Para calcular el seno hiperbólico de un número, simplemente tienes que escribir "Sinh" en el programa, donde "x" es el número del cual quieres calcular el seno hiperbólico.

Por ejemplo, si quieres calcular el seno hiperbólico de 2, puedes escribir "Sinh" en Mathematica. El programa evaluará esta expresión y te devolverá el valor exacto del seno hiperbólico de 2.

Es importante tener en cuenta que Mathematica utiliza radianes como unidad predeterminada para los ángulos. Por lo tanto, si quieres calcular el seno hiperbólico de un ángulo en grados, debes convertirlo a radianes antes de utilizar la función "Sinh". Puedes hacer esto multiplicando el ángulo en grados por Pi/180.

Con la función "Sinh", puedes calcular fácilmente el seno hiperbólico de cualquier número en Mathematica. Esta función es muy útil en cálculos relacionados con la física, la ingeniería y las matemáticas en general.

Cuál es la diferencia entre el coseno hiperbólico y el coseno tradicional

El coseno hiperbólico es una función matemática utilizada para calcular los valores hiperbólicos del coseno. A diferencia del coseno tradicional que está limitado a valores entre -1 y 1, el coseno hiperbólico puede tener valores positivos o negativos infinitos. Ya que el coseno hiperbólico es una función exponencial, su gráfica se asemeja a una curva suave y asintótica a medida que se acerca al infinito. Esto contrasta con la función coseno, cuya gráfica es una onda periódica. A continuación, veremos cómo calcular el coseno hiperbólico usando el lenguaje de programación Mathematica.

Cómo calcular el coseno hiperbólico en Mathematica

El lenguaje de programación Mathematica ofrece una función integrada llamada "Cosh" que permite calcular el coseno hiperbólico de un número. La sintaxis básica para el cálculo del coseno hiperbólico en Mathematica es la siguiente:

Cosh

Donde "x" representa el número para el cual deseamos encontrar el coseno hiperbólico. A continuación, presentaremos algunos ejemplos de cómo utilizar la función "Cosh" en Mathematica.

• Para calcular el coseno hiperbólico de 2, podemos escribir:

Cosh

• Esto devolverá el valor aproximado de 3.7621957.
• Para calcular el coseno hiperbólico de un número complejo, podemos escribir:

Cosh

• Esto devolverá el valor aproximado de -3.7245455 + 0.5118227I.
• Para calcular el coseno hiperbólico de una lista de números, podemos escribir:

Cosh

• Esto devolverá una lista con los valores aproximados de {1.54308, 3.7622, 10.0677}.

El coseno hiperbólico es una función matemática que permite calcular los valores hiperbólicos del coseno. Mathematica ofrece la función "Cosh" para calcular el coseno hiperbólico de un número o una lista de números.

Cuál es la diferencia entre el seno hiperbólico y el seno tradicional

El seno hiperbólico y el seno tradicional son dos conceptos relacionados pero distintos en matemáticas. Mientras que el seno tradicional se define en términos de la geometría de un círculo unitario, el seno hiperbólico se define en términos de la función exponencial.

El seno tradicional tiene un rango de valores entre -1 y 1, y se repite periódicamente cada 2π. Por otro lado, el seno hiperbólico puede tomar cualquier valor real y no se repite periódicamente.

Además, la relación entre el seno hiperbólico y el seno tradicional está dada por la fórmula:

senh(x) = (e^x - e^(-x)) / 2
sen(x) = (e^(ix) - e^(-ix)) / 2i

El seno hiperbólico y el seno tradicional son dos conceptos matemáticos relacionados pero distintos en términos de su definición y rango de valores.

Cuáles son las aplicaciones prácticas del coseno hiperbólico en matemáticas y ciencias

El coseno hiperbólico tiene numerosas aplicaciones en matemáticas y ciencias, especialmente en áreas como la física, la ingeniería y la estadística. Una de las aplicaciones más comunes es en el análisis de circuitos eléctricos, donde el coseno hiperbólico se utiliza para calcular las corrientes en circuitos complejos.

En física, el coseno hiperbólico también se aplica en el estudio del comportamiento de gases ideales, en la dinámica de fluidos y en la termodinámica. En ciencias de la computación, el coseno hiperbólico se utiliza en algoritmos de procesamiento de imágenes y en técnicas de aprendizaje automático para el reconocimiento de patrones.

Además, el coseno hiperbólico tiene aplicaciones en matemáticas puras, como en la teoría de números y en el estudio de funciones especiales. También es utilizado en la resolución de ecuaciones diferenciales lineales y en el cálculo de integrales.

Cuáles son las aplicaciones prácticas del seno hiperbólico en matemáticas y ciencias

El seno hiperbólico, abreviado como sinh, es una función matemática que se utiliza en diversas aplicaciones prácticas dentro de las matemáticas y las ciencias. Una de sus principales utilidades es en el cálculo de funciones y ecuaciones diferenciales no lineales. Además, el seno hiperbólico también se utiliza en el ámbito de la física, especialmente en el estudio de fenómenos ondulatorios y vibracionales. En matemáticas, el comportamiento del seno hiperbólico es de gran interés en la teoría de números y en la teoría de conjuntos. A continuación, exploraremos algunas aplicaciones prácticas más específicas del seno hiperbólico.

Cálculo de funciones y ecuaciones diferenciales

El seno hiperbólico es particularmente útil en el cálculo de funciones y ecuaciones diferenciales no lineales. Muchas funciones y sistemas físicos siguen una forma de comportamiento que puede describirse mediante ecuaciones diferenciales no lineales. En estos casos, el seno hiperbólico puede ser utilizado para resolver dichas ecuaciones y obtener soluciones numéricas o analíticas, dependiendo del caso. Esto permite modelar y comprender mejor el comportamiento de diversos fenómenos que van más allá de las funciones trigonométricas tradicionales.

Fenómenos ondulatorios y vibracionales

El seno hiperbólico también tiene aplicaciones en el estudio de fenómenos ondulatorios y vibracionales. Por ejemplo, en acústica, se utiliza para describir y analizar el comportamiento de las ondas sonoras en medios no lineales. Además, en electromagnetismo, el seno hiperbólico puede ser utilizado para representar el campo eléctrico o magnético en ciertos sistemas que exhiben comportamiento no lineal. Estas aplicaciones permiten comprender mejor cómo se propagan y se comportan las ondas en diferentes medios y materiales, lo cual es fundamental para el diseño y la optimización de dispositivos y sistemas.

Teoría de números y teoría de conjuntos

En matemáticas, el seno hiperbólico también es de gran interés en la teoría de números y la teoría de conjuntos. En la teoría de números, el seno hiperbólico aparece en el estudio de las funciones zeta de Riemann, que son de suma importancia en la teoría de números analítica. Además, en la teoría de conjuntos, el seno hiperbólico puede utilizarse para definir y analizar conjuntos que poseen propiedades especiales o que exhiben ciertos comportamientos no lineales. Estas aplicaciones muestran cómo el seno hiperbólico tiene implicaciones en distintas ramas de las matemáticas y cómo puede ser utilizado como una herramienta poderosa para el análisis y la resolución de problemas avanzados.

Existen otras funciones relacionadas con el coseno y seno hiperbólicos en Mathematica

Otra función relacionada es el coseno inverso hiperbólico, que se representa como ArcCosh. Esta función devuelve el valor del coseno hiperbólico inverso de x. Es importante destacar que este valor solo es válido para x >= 1. Si x es menor que 1, la función ArcCosh arrojará un error.

Por otro lado, tenemos la función seno inverso hiperbólico, que se representa como ArcSinh. Esta función devuelve el valor del seno hiperbólico inverso de x. A diferencia de ArcCosh, la función ArcSinh es válida para cualquier valor de x.

Además, existe la función tangente hiperbólica inversa, que se representa como ArcTanh. Esta función devuelve el valor de la tangente hiperbólica inversa de x. Al igual que ArcCosh, ArcTanh solo es válido para x que estén dentro del rango de -1 a 1.

Qué otros métodos o funciones puedo utilizar para calcular el coseno y seno hiperbólico en Mathematica

Además de las funciones incorporadas de Mathematica para calcular el coseno y seno hiperbólico, existen otros métodos y funciones que se pueden utilizar para obtener estos valores. Uno de ellos es utilizando la función de exponente exponencial y su inversa.

Por ejemplo, para calcular el coseno hiperbólico de un número x, puedes usar la fórmula:

cosh = (1/2) (Exp + Exp)

De manera similar, para calcular el seno hiperbólico de un número x, puedes usar la fórmula:

sinh = (1/2) (Exp - Exp)

Estas fórmulas son útiles cuando deseas calcular el coseno y seno hiperbólico de un número específico que no está incluido en las funciones incorporadas de Mathematica. Sin embargo, ten en cuenta que los resultados pueden no ser exactos debido a las limitaciones de la precisión numérica.

• También puedes utilizar las funciones hiperbólicas inversas, como la función arcocoseno hiperbólico (ArcCosh) y la función arcoseno hiperbólico (ArcSinh), para calcular los valores inversos del coseno y seno hiperbólico.
• Otra opción es utilizar la función Hypergeometric2F1, que es una función hipergeométrica que se puede utilizar para calcular el coseno y seno hiperbólico.
• Además, puedes utilizar la función de serie de Taylor para calcular una aproximación del coseno y seno hiperbólico.

Estas son solo algunas opciones adicionales que puedes explorar para calcular el coseno y seno hiperbólico en Mathematica. Experimenta con diferentes métodos y funciones para encontrar la más adecuada para tus necesidades.

Qué precauciones debo tomar al utilizar las funciones de coseno y seno hiperbólico en Mathematica

Al utilizar las funciones de coseno y seno hiperbólico en Mathematica, es importante tener en cuenta algunas precauciones. Primero, debes asegurarte de que los argumentos que ingreses estén en radianes, ya que Mathematica trabaja de forma predeterminada con radianes. Si tus datos están en grados, debes convertirlos antes de usar estas funciones.

Además, ten en cuenta que la función de coseno hiperbólico, cosh(x), puede producir valores muy grandes si el argumento x es grande. Esto puede llevar a errores de redondeo y pérdida de precisión. Si necesitas calcular el coseno hiperbólico para valores grandes, considera utilizar la función cosh(x) = (exp(x) + exp(-x))/2, que puede ser más precisa en estos casos.

Por otro lado, el seno hiperbólico, sinh(x), puede producir valores muy grandes si el argumento x también es grande. Si necesitas calcular el seno hiperbólico para valores grandes, puedes utilizar la función sinh(x) = (exp(x) - exp(-x))/2, que es más precisa en estos casos.

Finalmente, ten en cuenta que estas funciones pueden arrojar resultados complejos si el argumento es imaginario. Si necesitas trabajar con números complejos, asegúrate de utilizar la notación adecuada y tener esto en cuenta en tus cálculos.

Al utilizar las funciones de coseno y seno hiperbólico en Mathematica, recuerda asegurarte de que los argumentos estén en radianes, considerar las precauciones para valores grandes y tomar en cuenta la posibilidad de resultados complejos si el argumento es imaginario. Estas precauciones te ayudarán a obtener resultados más precisos y evitar posibles errores en tus cálculos.

Existen paquetes o bibliotecas adicionales en Mathematica que sean útiles para calcular funciones hiperbólicas

Sí, existen varios paquetes o bibliotecas adicionales en Mathematica que pueden ser útiles para calcular las funciones hiperbólicas, como el coseno y seno hiperbólico.

Uno de estos paquetes es el "HyperbolicFunctions`" que proporciona una variedad de funciones hiperbólicas, incluyendo el coseno y seno hiperbólico. Para utilizar este paquete, primero debes cargarlo utilizando la siguiente sintaxis:

Needs

A continuación, puedes utilizar las funciones hiperbólicas en tus cálculos. Por ejemplo, para calcular el coseno hiperbólico de un número, puedes usar la función "Cosh".

Además del paquete "HyperbolicFunctions`", también puedes utilizar la biblioteca de funciones integradas de Mathematica para calcular el coseno y seno hiperbólico. Para el coseno hiperbólico, puedes utilizar la función "Cosh", y para el seno hiperbólico, puedes utilizar la función "Sinh". Estas funciones están disponibles sin necesidad de cargar ningún paquete adicional.

Si necesitas calcular el coseno y seno hiperbólico en Mathematica, puedes utilizar tanto el paquete "HyperbolicFunctions`" como las funciones integradas de Mathematica. Ambas opciones te proporcionarán los resultados que necesitas.

Preguntas frecuentes (FAQ)

1) ¿Qué es el coseno hiperbólico?

El coseno hiperbólico es una función matemática que se utiliza para calcular los valores hiperbólicos de un número. Se denota como cosh(x).

2) ¿Qué es el seno hiperbólico?

El seno hiperbólico es una función matemática que se utiliza para calcular los valores hiperbólicos de un número. Se denota como sinh(x).

3) ¿Cómo puedo calcular el coseno hiperbólico en Mathematica?

Para calcular el coseno hiperbólico en Mathematica, puedes utilizar la función Cosh, donde x es el número del que deseas calcular el coseno hiperbólico.

4) ¿Cómo puedo calcular el seno hiperbólico en Mathematica?

Para calcular el seno hiperbólico en Mathematica, puedes utilizar la función Sinh, donde x es el número del que deseas calcular el seno hiperbólico.

5) ¿Qué es la función InverseCosh en Mathematica?

La función InverseCosh en Mathematica se utiliza para calcular el coseno hiperbólico inverso, es decir, el número cuyo coseno hiperbólico es igual a x. Se denota como ArcCosh.